7d05c06f-a9
UFSCAR 2007 - Matemática - Funções, Logaritmos
Adotando-se log 2 = a e log 3 = b, o valor de 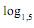 135 é igual a
135 é igual a
Adotando-se log 2 = a e log 3 = b, o valor de 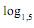 135 é igual a
135 é igual a
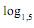 135 é igual a
135 é igual aA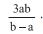
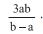
B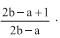
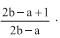
C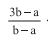
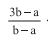
D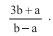
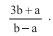
E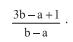
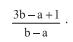
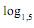 135 é igual a
135 é igual a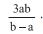
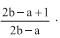
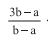
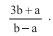
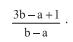
 formam, nesta ordem, uma progressão aritmética, com
formam, nesta ordem, uma progressão aritmética, com  então o valor de
então o valor de 
 então o determinante da matriz A é igual a
então o determinante da matriz A é igual a
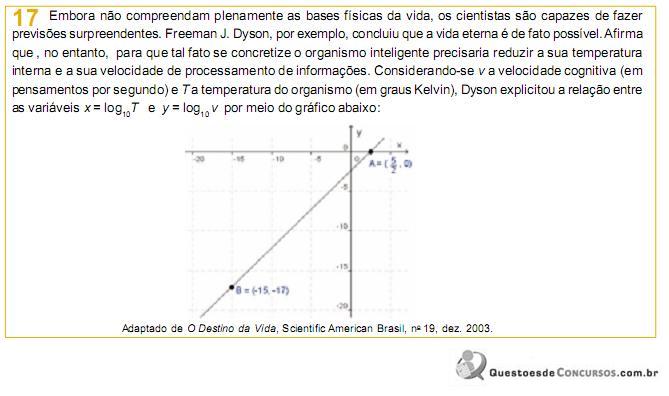
 em que
em que  é a concentração de íons, dada em mol por litro.
é a concentração de íons, dada em mol por litro. e M0 = 4 g, então, depois de 4 anos, a massa da amostra será inferior a 2 g.
e M0 = 4 g, então, depois de 4 anos, a massa da amostra será inferior a 2 g. em anos, pela expressão
em anos, pela expressão









 0,30, log10 3
0,30, log10 3  0,48, então o maior número inteiro n, satisfazendo 10n ≤ 12418, é igual a
0,48, então o maior número inteiro n, satisfazendo 10n ≤ 12418, é igual a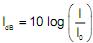 , onde I 0 = 10–12 W/m2 representa a intensidade sonora de referência de um som muito fraco percebido pelo ouvido humano.
, onde I 0 = 10–12 W/m2 representa a intensidade sonora de referência de um som muito fraco percebido pelo ouvido humano.