Segundo reportagem da
Revista Aquecimento Global (ano 2, n. 8, 2009, p. 20-23), o acordo ambiental conhecido como “20-20-20”, assinado por representantes dos países membros da União Europeia, sugere que, até 2020, todos os países da comunidade reduzam em 20% a emissão de dióxido de carbono

em relação ao que cada país emitiu em 1990.
Suponha que em certo país o total estimado de

emitido em 2009 foi 28% maior que em 1990. Com isso, após o acordo, esse país estabeleceu a meta de reduzir sua emissão de

ano após ano, de modo que a razão entre o total emitido em um ano n

e o total emitido no ano anterior

seja constante, começando com a razão

até

atingindo em 2020 a redução preconizada pelo acordo. Assim, essa razão de redução será de:

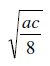
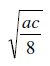
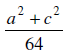
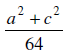
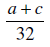
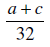
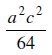
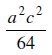
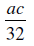
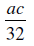







 defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por
defina, para x ≠ 0, g(x) por g(x) = log3f(x). O conjunto imagem de g, dado por 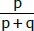 é
é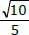
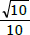
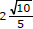
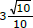
 = k podemos afirmar, corretamente, que a soma das raízes da equação 2x - 12 + 27.2 -x = 0 é igual a
= k podemos afirmar, corretamente, que a soma das raízes da equação 2x - 12 + 27.2 -x = 0 é igual a  em relação ao que cada país emitiu em 1990.
em relação ao que cada país emitiu em 1990. emitido em 2009 foi 28% maior que em 1990. Com isso, após o acordo, esse país estabeleceu a meta de reduzir sua emissão de
emitido em 2009 foi 28% maior que em 1990. Com isso, após o acordo, esse país estabeleceu a meta de reduzir sua emissão de  ano após ano, de modo que a razão entre o total emitido em um ano n
ano após ano, de modo que a razão entre o total emitido em um ano n  e o total emitido no ano anterior
e o total emitido no ano anterior  seja constante, começando com a razão
seja constante, começando com a razão  até
até  atingindo em 2020 a redução preconizada pelo acordo. Assim, essa razão de redução será de:
atingindo em 2020 a redução preconizada pelo acordo. Assim, essa razão de redução será de: 








 e supondo-se que, em meio rico em triptofano, a população de 0 bactérias selvagens no instante t =
e supondo-se que, em meio rico em triptofano, a população de 0 bactérias selvagens no instante t =  é igual a 6 mil 0 indivíduos, então
é igual a 6 mil 0 indivíduos, então  = 2,375 horas.
= 2,375 horas.


