A Figura 1 ilustra duas moedas brasileiras, a
de R$ 1,00 e a de R$ 0,50, descritas abaixo.

Figura 1: Moedas brasileiras
Moeda de R$ 1,00 – As faces da moeda são
compostas por dois círculos concêntricos. O
diâmetro do círculo maior é igual a 2,8 cm e o
diâmetro do círculo menor é igual a 1,8 cm. A
espessura desta moeda é igual a 1,5 mm.
Moeda de R$ 0,50 – As faces da moeda são
compostas por um círculo de diâmetro igual a
2,2 cm. A espessura desta moeda é igual a 3 mm.
Com base nestas informações, analise as
proposições abaixo.
I. O volume de metal necessário para cunhar
a região situada entre os círculos
concêntricos da moeda de R$ 1,00 é
aproximadamente 0,1725 π cm3
.
II. Para cunhar uma moeda de R$ 1,00 é
necessário aproximadamente 0,069 π cm3
de metal a mais que para cunhar uma
moeda de R$ 0,50.
III. A área entre os círculos concêntricos da
moeda de R$ 1,00 é 0,34 π cm2 maior que
a do círculo interno.
Assinale a alternativa correta.

 e BC = 12 cm, a área do triângulo ABC é igual a:
e BC = 12 cm, a área do triângulo ABC é igual a: 
 e BC = 12 cm, a área do triângulo ABC é igual a:
e BC = 12 cm, a área do triângulo ABC é igual a: 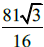 cm³, então sua área superficial total é de aproximadamente:
cm³, então sua área superficial total é de aproximadamente:
 , o ponto
médio da diagonal
AC. O produto
, o ponto
médio da diagonal
AC. O produto



 mede 2 cm e os ângulos
mede 2 cm e os ângulos  e
e  medem, respectivamente,
60º
e
75º
, então a
área e o perímetro deste triângulo são,
respectivamente:
medem, respectivamente,
60º
e
75º
, então a
área e o perímetro deste triângulo são,
respectivamente:


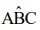 = 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3.
= 60º e com distância de 6 cm entre as
bases, como mostra a Figura 3. 
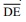 mede 10 cm, a área do trapézio é:
mede 10 cm, a área do trapézio é:


