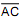b236b59a-a6
FGV 2015, FGV 2015 - Matemática - Áreas e Perímetros, Geometria Plana
No intervalo de 0 a π, a função que permite calcular a área
A da região limitada pelo eixo x, pelas retas de equações
x = p e x = q e pelo gráfico da função definida por y = sen x é
dada por A = cos p – cos q.

Com base na informação fornecida, observe a figura a seguir.

A área da região sombreada nessa figura é, aproximadamente,
igual a
No intervalo de 0 a π, a função que permite calcular a área
A da região limitada pelo eixo x, pelas retas de equações
x = p e x = q e pelo gráfico da função definida por y = sen x é
dada por A = cos p – cos q.

Com base na informação fornecida, observe a figura a seguir.

A área da região sombreada nessa figura é, aproximadamente, igual a

Com base na informação fornecida, observe a figura a seguir.

A área da região sombreada nessa figura é, aproximadamente, igual a
A
2,64.
B
2,14.
C
1,86.
D
1,14.
E
0,86.
 é perpendicular a
é perpendicular a  , e a medida do ângulo
entre
, e a medida do ângulo
entre  e a reta s é 30°.
e a reta s é 30°.
 , em cm, é igual a
, em cm, é igual a e
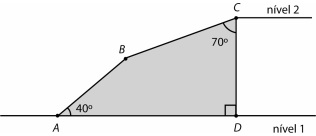
e  de uma circunferência de centro O são,
respectivamente, lados de polígonos regulares de 6 e 10
lados inscritos nessa circunferência. Na mesma circunferência,
as cordas
de uma circunferência de centro O são,
respectivamente, lados de polígonos regulares de 6 e 10
lados inscritos nessa circunferência. Na mesma circunferência,
as cordas  e
e  se intersectam no ponto P, conforme
indica a figura a seguir.
se intersectam no ponto P, conforme
indica a figura a seguir.
 , indicado na figura por α, é igual a
, indicado na figura por α, é igual a


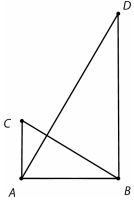
 , e
, e  representa uma corda perfeitamente esticada, inicialmente perpendicular à parede.
representa uma corda perfeitamente esticada, inicialmente perpendicular à parede.
 .
. , e o ângulo
, e o ângulo  é reto.
é reto.