Questõesde Esamc sobre Geometria Plana

InícioTodas as questões
1
1
1
Foram encontradas 33 questões
96aaa8b0-e6
Esamc 2016 - Matemática - Áreas e Perímetros, Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos

Na figura, MNQR é um quadrado, o segmento MP contém o ponto Q, o ângulo ONP mede 60° e a razão MN/NO é igual a 1/2. Sabendo que a diagonal do quadrado mede 6√2 CM cm, pode-se afirmar que a distância entre os pontos N e P, em cm, é igual a:



A
6(√3 - 1)
B
6√3
C
3(√2 - 1)
D
6(√3 + 1)
E
(√2 + 1) 
968c7254-e6
Esamc 2016 - Matemática - Áreas e Perímetros, Polígonos, Geometria Plana

Um procedimento utilizado para o cálculo de áreas de polígonos não regulares é a soma das áreas de triângulos não-sobrepostos internos ao polígono cuja reunião seja equivalente ao próprio polígono. Nesses casos, é de grande valia a utilização da “fórmula de Herão”, dada por A = √ S.(s - a) . (s - b) . (s - c) em que s = a + b +c/2 que determina a área A do triângulo cujos lados medem a, b e c.

Utilizando o procedimento descrito acima, pode-se afirmar que a área (em m²) da figura abaixo, construída fora de escala, pertence a qual dos intervalos?




A
[9,18]
B
]18,27]
C
]27, 36]
D
]36, 45]
E
]45, 54]
50e6b593-df
Esamc 2015 - Matemática - Pontos e Retas, Geometria Analítica, Polígonos, Geometria Plana, Triângulos

Na fi gura a seguir, ABCD é um retângulo e o ponto E é a interseção dos segmentos 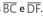. Se BE = 2; CE, EF = 2; DE, AB = 4 cm e AD = 9 cm, qual das medidas a seguir mais se aproxima de CF?



A
09
B
10
C
11
D
12
E
13
50dfb078-df
Esamc 2015 - Matemática - Álgebra, Áreas e Perímetros, Problemas, Geometria Plana

Na pizzaria “Bela Itália”, todas as pizzas possuem o mesmo tamanho (20 cm de raio) e são vendidas a preço único de R$ 60,00. O proprietário da pizzaria, com o objetivo de aumentar seu lucro, diminuiu o raio das pizzas em 1 cm, mantendo o preço inalterado. Sabendo-se que o custo médio de produção de cada pizza é de 2 centavos/cm², e adotando-se π = 3, pode-se afirmar que essa alteração elevou o lucro de cada unidade vendida em:

A
R$ 1,94
B
R$ 2,04
C
R$ 2,14
D
R$ 2,24
E
R$ 2,34
50e310dc-df
Esamc 2015 - Matemática - Áreas e Perímetros, Geometria Plana

No plano cartesiano, considerando a unidade de medida como sendo 1 centímetro, a área da região determinada por



é igual a:

A
7,5 cm²
B
9 cm²
C
13,5 cm²
D
16 cm²
E
18 cm²
50cd6d24-df
Esamc 2015 - Matemática - Circunferências e Círculos, Polígonos, Geometria Plana

Na fi gura abaixo, o ponto O é o centro da circunferência maior e vértice do quadrado MNOP, de lado igual a 1. O raio da circunferência menor, tangente à circunferência maior e aos lados do quadrado, é igual a:



A
√2 - 1
B
1/4
C
√2/4
D
2-√2/2
E
3-2√2
50c79436-df
Esamc 2015 - Matemática - Polígonos, Geometria Plana, Análise Combinatória em Matemática

João é um artista plástico que dispõe de cinco cores diferentes e deseja pintar o quadro, dividido em 5 regiões distintas:



Para pintar o quadro, João deve respeitar duas regras:


I. Cada região deve ser pintada com uma única cor;
II. Duas regiões vizinhas (cuja fronteira é um segmento de reta) devem ter, necessariamente, cores distintas.


O número de maneiras distintas que João poderá colorir o quadro é:

A
540
B
420
C
360
D
240
E
120
c18ef146-f2
Esamc 2018 - Matemática - Áreas e Perímetros, Geometria Plana

Para a premiação dos 3 melhores classificados numa olimpíada científica, foi construído um pódio em formato de prisma, cujas faces (inclusive a inferior e a posterior) foram feitas com placas de madeira contendo apenas ângulos retos, conforme a figura.



Qual dos valores abaixo fica mais próximo do valor total gasto com as placas de madeira, sabendo que não houve desperdício e que foram compradas por R$ 30,00/m²?

A
R$ 150,00
B
R$ 190,00
C
R$ 230,00
D
R$ 170,00
E
R$ 210,00
c184177b-f2
Esamc 2018 - Matemática - Circunferências e Círculos, Geometria Plana

Deseja-se confeccionar um adereço de um colar que represente a cabeça de uma águia. Para isso, foram desenhadas duas semicircunferências, de modo que o diâmetro da menor estivesse contido no diâmetro da maior e o centro da maior pertencesse à menor.


Esse adereço deverá conter uma pequena pedra de diamante com formato circular, para representar o olho da águia. Essa pedra tangenciará todas as bordas do adereço, conforme ilustra a figura abaixo:



Se o raio da semicircunferência maior mede 4 cm, então o raio da pedra de diamante medirá:

A
11/6 cm.
B
16/9 cm.
C
√13/7 cm.
D
√15/9 cm.
E
2/3 cm.
ffb1379b-f0
Esamc 2019 - Matemática - Áreas e Perímetros, Geometria Plana

Para fiscalizar a segurança de moradias em áreas de risco de desabamentos, um drone fotografa a região e, a partir da foto, localiza cada ponto desta região por meio de um sistema de coordenadas cartesianas.



Uma determinada região foi representada no sistema cartesiano formando o pentágono OABCD, com as coordenadas de seus vértices descritas na figura a seguir:

Com o intuito de otimizar a fiscalização desta região, esse drone dividiu-a em duas regiões menores, com áreas iguais, por meio de uma reta vertical, o que permitiu duas equipes de fiscalização trabalharem simultaneamente.

A reta que delimita a região em que cada uma das equipes trabalhou possui equação

A
x = 38 - √860
B
x = √195 -10
C
x = 19 + √215
D
x = √430 -15
E
x = 19 - √215
ffb9f21a-f0
Esamc 2019 - Matemática - Áreas e Perímetros, Geometria Plana

A geometria do incêndio florestal

    A superfície afetada pela propagação do incêndio tem formas geométricas distintas em função dos fatores que interferem na propagação do fogo. Nos incêndios em áreas planas, com combustíveis uniformes e contínuos, a propagação tenderá a uma forma circular. Sob a ação do vento, pode transformar-se em elipsoidal.


(“Investigação de Incêndios Florestais”, do Instituto Brasileiro do Meio Ambiente e dos Recursos Naturais Renováveis. Ministério do Meio Ambiente. Página 32.)

Um dos problemas da fiscalização nos combates a focos de incêndios florestais é o tempo necessário para se identificar um foco de incêndio: uma determinada tecnologia detecta o incêndio quando este atinge uma área mínima de 6000 km2 

Suponha que um foco de incêndio possua área inicial de 3 km2 e se propague de forma circular, com a medida de seu raio aumentando constantemente à velocidade de 4 km/h. Assim, o tempo mínimo necessário para que essa tecnologia detecte o incêndio está entre:

(Nesta questão, considere π ≈ 3)

A
9 e 10 horas.
B
10 e 11 horas.
C
11 e 12 horas.
D
12 e 13 horas.
E
13 e 14 horas.
ff9bcd78-f0
Esamc 2019 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos

Para determinar a distância entre os pontos A e O, um topógrafo, posicionado em E, mediu o ângulo OEA e obteve 57º . Em seguida, caminhou 60 m até o ponto O e mediu o ângulo AÔE, obtendo 59º , conforme a figura.



Adotando sen 57º = 0,83, sen 59º = 0,85 e sen 64º = 0,90 pode-se afirmar que a distância, em metros, entre os pontos A e O, determinada corretamente pelo topógrafo, fica mais próxima de:

A
55
B
57
C
59
D
61
E
63
ff794db7-f0
Esamc 2019 - Matemática - Áreas e Perímetros, Funções, Geometria Plana, Função de 2º Grau

Na figura a seguir, o retângulo ABCD tem dois vértices na parábola que correspondem ao gráfico da função f (x) = - (x - 1) . (x - 6) e dois vértices no eixo das abscissas.

Sabendo que as coordenadas do vértice D são (5,0), o perímetro do retângulo ABCD é:


A
12
B
14
C
16
D
18
E
20
ff71dbc0-f0
Esamc 2019 - Matemática - Áreas e Perímetros, Geometria Plana

A utilização de softwares destinados à construção de gráficos matemáticos é uma prática comum entre alunos de diversos cursos de nível superior como, por exemplo, engenharia e economia. Durante a execução de um trabalho proposto, um aluno utilizou um software para encontrar a região do plano cartesiano que satisfazia, simultaneamente, as seguintes condições: (x - 2)2 + (y - 2)2 ≥ 4, 0 ≤ x ≤ 4 e 0 ≤ t ≤ 4. A área dessa região do plano é

A
4 (4 - π)
B
4 - π
C
16 - 2π
D
4 + 2π
E
16 - π
29bcd78e-de
Esamc 2014 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos

No triângulo ABC, retângulo em Â, o ângulo mede 30 . Os segmentos são, respectivamente, a altura e a mediana relativas ao vértice A. Os segmentos são, respectivamente, as bissetrizes dos ângulos

Nessas condições, pode-se afirmar que o ângulo mede:


A
85o
B
90o
C
95o
D
100o
E
105o
29b9682b-de
Esamc 2014 - Matemática - Áreas e Perímetros, Geometria Plana

Para terminar o projeto da reforma de um apartamento, a arquiteta responsável precisa determinar o perímetro da sala apresentada na figura a seguir, feita fora de escala. Sabendo-se que a área total da sala é igual a 48 m², pode-se afirmar que o perímetro procurado, em metros, é igual a:



A
38
B
36
C
34
D
32
E
30
299e73b9-de
Esamc 2014 - Matemática - Circunferências e Círculos, Polígonos, Geometria Plana

Carlos pretende transportar o maior número possível de latas de óleo ci- Espaço Para Rascunho líndricas em uma caixa em formato de paralelepípedo reto-retângulo. As latas viajarão deitadas (eixos dos cilindros paralelos ao chão) e suas bases ocuparão um retângulo com dimensões 60 cm por 55 cm, com as arestas de 60 cm na posição horizontal (tomando o chão como referência). Carlos está na dúvida entre duas disposições possíveis, como sugerem os acondicionamentos incompletos representados pelas figuras abaixo:



Sabendo que os diâmetros das bases das latas medem 10 cm, a melhor opção para Carlos é a disposição:

A
A, pois caberão 8 latas a mais do que na disposição B.
B
A, pois caberão 5 latas a mais do que na disposição B.
C
A, pois caberão 2 latas a mais do que na disposição B.
D
B, pois caberão 5 latas a mais do que na disposição A.
E
B, pois caberão 3 latas a mais do que na disposição A.
29a5e0e7-de
Esamc 2014 - Matemática - Áreas e Perímetros, Geometria Plana, Triângulos

Um terreno plano de forma triangular é determinado pelos pontos P, F e R. Sabe-se que a distância entre P e F é de 120 m e que os ângulos PRF e RPF, medem, respectivamente, 120° e 45°. Para cercar o terreno por completo, a extensão mínima da cerca deve ser um número compreendido entre:

A
240 m e 270 m
B
270 m e 300 m
C
300 m e 330 m
D
330 m e 360 m
E
360 m e 390 m
29a181fd-de
Esamc 2014 - Matemática - Áreas e Perímetros, Circunferências e Círculos, Geometria Plana, Triângulos

Passando pelo centro da circunferência C1 de equação cartesiana x² + y² 6x 8y + 23 = 0, a reta r é, também, perpendicular à reta y = x. Uma circunferência C2, concêntrica com a primeira, é tangente ao eixo Oy no ponto P. A área do triângulo cujos vértices são o ponto P e os pontos de intersecção da reta r com C1 é:

A
1
B
2 √2
C
3
D
√10
E
5
4a8d8ca9-dc
Esamc 2013 - Matemática - Circunferências e Círculos, Geometria Plana

Na circunferência a seguir, a corda BC mede 10 cm e o ângulo BÂC mede 150º. O comprimento da circunferência, em cm, é igual a:


A
5 π
B
5 √3 π
C
10 π
D
10 √3 π
E
20 π