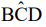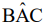942eb67a-05
UFRGS 2016 - Matemática - Circunferências e Círculos, Geometria Plana, Ângulos - Lei Angular de Thales, Triângulos
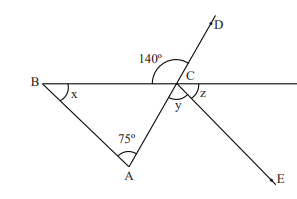
Um desenhista foi interrompido durante a
realização de um trabalho, e seu desenho
ficou como na figura abaixo.

Se o desenho estivesse completo, ele seria
um polígono regular composto por triângulos
equiláteros não sobrepostos, com dois de
seus vértices sobre um círculo, e formando
um ângulo de 40º, como indicado na figura.
Quando a figura estiver completa, o número de
triângulos equiláteros com dois de seus
vértices sobre o círculo é
Um desenhista foi interrompido durante a
realização de um trabalho, e seu desenho
ficou como na figura abaixo.

Se o desenho estivesse completo, ele seria
um polígono regular composto por triângulos
equiláteros não sobrepostos, com dois de
seus vértices sobre um círculo, e formando
um ângulo de 40º, como indicado na figura.
Quando a figura estiver completa, o número de
triângulos equiláteros com dois de seus
vértices sobre o círculo é
A
10.
B
12.
C
14.
D
16.
E
18.