Questõesde ENEM sobre Equações Exponenciais

InícioTodas as questões
1
1
1
Foram encontradas 10 questões
68a8fab0-7c
ENEM 2020 - Matemática - Funções, Equações Exponenciais

Um laboratório realizou um teste para calcular a velocidade de reprodução de um tipo de bactéria. Para tanto, realizou um experimento para observar a reprodução de uma quantidade x dessas bactérias por um período de duas horas. Após esse período, constava no habitáculo do experimento uma população de 189 440 da citada bactéria. Constatou-se, assim, que a população de bactérias dobrava a cada 0,25 hora.

A quantidade inicial de bactérias era de

A
370.
B
740.
C
1 480.
D
11 840.
E
23 680.
9edf1d9f-5f
ENEM 2020 - Matemática - Funções, Equações Exponenciais

    Enquanto um ser está vivo, a quantidade de carbono 14 nele existente não se altera. Quando ele morre, essa quantidade vai diminuindo. Sabe-se que a meia-vida do carbono 14 é de 5 730 anos, ou seja, num fóssil de um organismo que morreu há 5 730 anos haverá metade do carbono 14 que existia quando ele estava vivo. Assim, cientistas e arqueólogos usam a seguinte fórmula para saber a idade de um fóssil encontrado: Q(f) = Q0 . 2-t/5730 em que t é o tempo, medido em ano, Q(f) é a quantidade de carbono 14 medida no instante t e Q0 é a quantidade de carbono 14 no ser vivo correspondente.

Um grupo de arqueólogos, numa de suas expedições, encontrou 5 fósseis de espécies conhecidas e mediram a quantidade de carbono 14 neles existente. Na tabela temos esses valores juntamente com a quantidade de carbono 14 nas referidas espécies vivas.





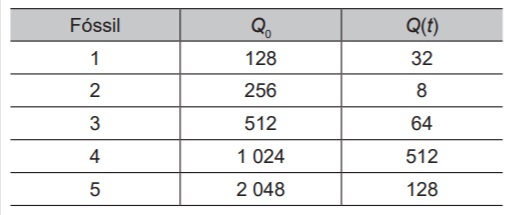
O fóssil mais antigo encontrado nessa expedição foi

A
1.
B
2.
C
3.
D
4.
E
5.
1aaaaca2-4b
ENEM 2014 - Matemática - Equações Exponenciais

Pesquisas indicam que o número de bactérias X é duplicado a cada quarto de hora. Um aluno resolveu fazer uma observação para verificar a veracidade dessa afirmação. Ele usou uma população inicial de 105 bactérias X e encerrou a observação ao final de uma hora.

Suponha que a observação do aluno tenha confirmado que o número de bactérias X se duplica a cada quarto de hora.

Após uma hora do início do período de observação desse aluno, o número de bactérias X foi de

A
2-2 . 105
B
2-1 . 105
C
22 . 105
D
23 . 105
E
24 . 105
10068b31-4e
ENEM 2013 - Matemática - Funções, Equações Exponenciais

Em um experimento, uma cultura de bactérias tem sua população reduzida pela metade a cada hora, devido à ação de um agente bactericida.


Neste experimento, o número de bactérias em função do tempo pode ser modelado por uma função do tipo

A
afim.
B
seno.
C
cosseno.
D
logarítmica crescente.
E
exponencial.
1e7913e7-4c
ENEM 2011 - Matemática - Funções, Equações Exponenciais

A torre de Hanói é um jogo que tem o objetivo de mover todos os discos de uma haste para outra, utilizando o menor número possível de movimento, respeitando-se as regras.



As regras são:

1- um disco maior não pode ser colocado sobre um disco menor;

2- pode-se mover um único disco por vez;

3- um disco deve estar sempre em uma das três hastes ou em movimento.

Disponível em: http://www.realidadevirtual.com.br. Acesso em: 28 abr. 2010 (adaptado).

Disponível em: http://www.imeusp.br. Acesso em: 28 abr. 2010 (adaptado).


Usando a torre de Hanói e baseando-se nas regras do jogo, podemos montar uma tabela entre o número de peças (X) e o número mínimo de movimentos (Y):



A relação entre (X) e (Y) é

A
Y = 2X - 1
B
Y = 2X-1
C
Y = 2X
D
Y = 2X - 1
E
Y = 2X - 4
f81943cb-4a
ENEM 2015 - Matemática - Funções, Equações Exponenciais

O sindicato de trabalhadores de uma empresa sugere que o piso salarial da classe seja de R$ 1 800,00, propondo um aumento percentual fixo por cada ano dedicado ao trabalho. A expressão que corresponde à proposta salarial (s), em função do tempo de serviço (t), em anos, é s(t) = 1 800  (1,03)t .


De acordo com a proposta do sindicato, o salário de um profissional de empresa com 2 anos de tempo de serviço será, em reais,

A
7 416,00.
B
3 819,24.
C
3 709,62.
D
3 708,00.
E
1 909,62.
434d88f1-be
ENEM 2016 - Matemática - Funções, Equações Exponenciais, Inequação Logarítmica

Admita que um tipo de eucalipto tenha expectativa de crescimento exponencial, nos primeiros anos após seu plantio, modelado pela função y(t) = at -1, na qual y representa a altura da planta em metro, t é considerado em ano, e a é uma constante maior que 1 . O gráfico representa a função y.

Admita ainda que y(0) fornece a altura da muda quando plantada, e deseja-se cortar os eucaliptos quando as mudas crescerem 7,5 m após o plantio.

O tempo entre a plantação e o corte, em ano, é igual a

A
3.
B
4.
C
6 .
D
log2 7.
E
log2 15.
42afa14e-be
ENEM 2016 - Matemática - Funções, Equações Exponenciais

O governo de uma cidade está preocupado com a possível epidemia de uma doença infectocontagiosa causada por bactéria. Para decidir que medidas tomar, deve calcular a velocidade de reprodução da bactéria. Em experiências laboratoriais de uma cultura bacteriana, inicialmente com 40 mil unidades, obteve-se a fórmula para a população:

p(t) = 40 • 23t em que t é o tempo, em hora, e p(t) é a população, em milhares de bactérias.

Em relação à quantidade inicial de bactérias, após 20 min, a população será

A
reduzida a um terço.
B
reduzida à metade.
C
reduzida a dois terços.
D
duplicada.
E
triplicada.
96ff6981-7f
ENEM 2015 - Matemática - Funções, Equações Exponenciais

  O acréscimo de tecnologias no sistema produtivo industrial tem por objetivo reduzir custos e aumentar a produtividade. No primeiro ano de funcionamento, uma indústria fabricou 8.000 unidades de um determinado produto. No ano seguinte, investiu em tecnologia adquirindo novas máquinas e aumentou a produção em 50%.Estima-se que esse aumento percentual se repita nos próximos anos, garantindo um crescimento anual de 50%.Considere P a quantidade anual de produtos fabricados no ano t de funcionamento da indústria.

Se a estimativa for alcançada, qual é a expressão que determina o número de unidades produzidas P em função e t, para t ≥ 1?


A
P(t) = 0,5 . t -1 + 8 000
B
P(t) = 50 . t -1 + 8 000
C
P(t) = 4 000 . t -1 + 8 000
D
P(t) = 8 000 . (0,5) t-1
E
P(t) = 8 000 . (1,5) t-1
1eb45538-54
ENEM 2009 - Matemática - Equações Exponenciais

Texto para as questões 138 e 139

A população mundial está ficando mais velha, os índices de natalidade diminuíram e a expectativa de vida aumentou. No gráfico seguinte, são apresentados dados obtidos por pesquisa realizada pela Organização das Nações Unidas (ONU), a respeito da quantidade de pessoas com 60 anos ou mais em todo o mundo. Os números da coluna da direita representam as faixas percentuais. Por exemplo, em 1950 havia 95 milhões de pessoas com 60 anos ou mais nos países desenvolvidos, número entre 10% e 15% da população total nos países desenvolvidos.

Imagem 028.jpg

Suponha que o modelo exponencial y = 363e 0,03X, em que x = 0 corresponde ao ano 2000, x = 1 corresponde ao ano 2001, e assim sucessivamente, e que y é a população em milhões de habitantes no ano x, seja usado para estimar essa população com 60 anos ou mais de idade nos países em desenvolvimento entre 2010 e 2050. Desse modo, considerando e 0,3 = 1,35, estima-se que a população com 60 anos ou mais estará, em 2030, entre

A
490 e 510 milhões.
B
550 e 620 milhões.
C
780 e 800 milhões.
D
810 e 860 milhões.
E
870 e 910 milhões.