Questõesde USP sobre Funções
Um comerciante adotou como forma de pagamento uma
máquina de cartões, cuja operadora cobra uma taxa de 6% em
cada venda. Para continuar recebendo exatamente o mesmo
valor por cada produto, ele resolveu aplicar um reajuste nos
preços de todos os produtos da loja. Se P era o valor de uma
mercadoria antes da adoção da máquina, o novo valor V deve
ser calculado por
Se a função ƒ:ℝ - {2} →ℝ é definida por ݂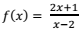 e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
Se a função ƒ:ℝ - {2} →ℝ é definida por ݂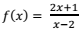 e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
Sejam Df e Dg os maiores subconjuntos de ℝ nos quais estão
definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g , respectivamente.
Nessas condições,
Sejam Df e Dg os maiores subconjuntos de ℝ nos quais estão definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g , respectivamente.
Nessas condições,
Sejam ƒ:ℝ → ℝ e g: ℝ+ → definidas por

respectivamente.
O gráfico da função composta g °ƒ é:
Sejam ƒ:ℝ → ℝ e g: ℝ+ → definidas por

respectivamente.
O gráfico da função composta g °ƒ é:





Uma quantidade fixa de um gás ideal é mantida a
temperatura constante, e seu volume varia com o tempo de
acordo com a seguinte fórmula:
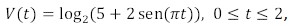
em que t é medido em horas e V(t) é medido em m3. A
pressão máxima do gás no intervalo de tempo [0,2] ocorre
no instante
Uma quantidade fixa de um gás ideal é mantida a temperatura constante, e seu volume varia com o tempo de acordo com a seguinte fórmula:
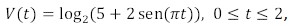
em que t é medido em horas e V(t) é medido em m3. A
pressão máxima do gás no intervalo de tempo [0,2] ocorre
no instante
Considere as funções 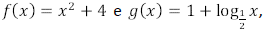 em que o domínio de f é o conjunto dos números reais e o
domínio de g é o conjunto dos números reais maiores do
que 0. Seja
em que o domínio de f é o conjunto dos números reais e o
domínio de g é o conjunto dos números reais maiores do
que 0. Seja

em que x > 0. Então, h(2) é igual a
Considere as funções 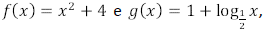 em que o domínio de f é o conjunto dos números reais e o
domínio de g é o conjunto dos números reais maiores do
que 0. Seja
em que o domínio de f é o conjunto dos números reais e o
domínio de g é o conjunto dos números reais maiores do
que 0. Seja

em que x > 0. Então, h(2) é igual a
Use as propriedades do logaritmo para simplificar a expressão  O valor de S é
O valor de S é

Diz-se que dois pontos da superfície terrestre são antípodas
quando o segmento de reta que os une passa pelo centro
da Terra.
Podem ser encontradas, em sites da internet,
representações, como a reproduzida abaixo, em que as
áreas escuras identificam os pontos da superfície terrestre
que ficam, assim como os seus antípodas, sobre terra firme.
Por exemplo, os pontos antípodas de parte do sul da
América do Sul estão no leste da Ásia.

Se um ponto tem latitude x graus norte e longitude y graus
leste, então seu antípoda tem latitude e longitude,
respectivamente,
Podem ser encontradas, em sites da internet, representações, como a reproduzida abaixo, em que as áreas escuras identificam os pontos da superfície terrestre que ficam, assim como os seus antípodas, sobre terra firme. Por exemplo, os pontos antípodas de parte do sul da América do Sul estão no leste da Ásia.

Se um ponto tem latitude x graus norte e longitude y graus leste, então seu antípoda tem latitude e longitude, respectivamente,
Seja f uma função a valores reais, com domínio  tal que
tal que
f ( x ) = log10 ( log 1/3 ( x2 - x + 1 ) ) , para todo 

O conjunto que pode ser o domínio D é
 tal que
tal que f ( x ) = log10 ( log 1/3 ( x2 - x + 1 ) ) , para todo


O conjunto que pode ser o domínio D é





Sobre a equação (x + 3)2x2 - 9 log | x2 + x — 1| = 0, é correto afirmar que
O número real x, com 0 < x < π , satisfaz a equação


Uma substância radioativa sofre desintegração ao


Considere a função
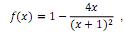
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
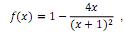
a qual está definida para x ≠ - 1. Então para todo x ≠ 1 e x ≠ - 1 , o produto f (x) f (-x) é igual a
Sejam  A soma dos valores absolutos das raízes da equação
A soma dos valores absolutos das raízes da equação  é igual a
é igual a
 A soma dos valores absolutos das raízes da equação
A soma dos valores absolutos das raízes da equação  é igual a
é igual aA função f :  tem como gráfico uma parábola e satisfaz f ( x + 1 ) - f (x) = 6 x - 2, para todo número real x.Então, o menor valor de f (x) ocorre quando x é igual a
tem como gráfico uma parábola e satisfaz f ( x + 1 ) - f (x) = 6 x - 2, para todo número real x.Então, o menor valor de f (x) ocorre quando x é igual a
 tem como gráfico uma parábola e satisfaz f ( x + 1 ) - f (x) = 6 x - 2, para todo número real x.Então, o menor valor de f (x) ocorre quando x é igual a
tem como gráfico uma parábola e satisfaz f ( x + 1 ) - f (x) = 6 x - 2, para todo número real x.Então, o menor valor de f (x) ocorre quando x é igual a



Tendo em vista as aproximações log10 2  0,30, log10 3
0,30, log10 3  0,48, então o maior número inteiro n, satisfazendo 10n ≤ 12418, é igual a
0,48, então o maior número inteiro n, satisfazendo 10n ≤ 12418, é igual a
 0,30, log10 3
0,30, log10 3  0,48, então o maior número inteiro n, satisfazendo 10n ≤ 12418, é igual a
0,48, então o maior número inteiro n, satisfazendo 10n ≤ 12418, é igual a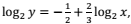 para x > 0, então
para x > 0, então 





