Questõessobre Funções Trigonométricas e Funções Trigonométricas Inversas
Considere os números complexos:

Então, sobre o produto y . (-ix), podemos afirmar que:
Considere os números complexos:

Então, sobre o produto y . (-ix), podemos afirmar que:
Considere θ um número real qualquer. Sobre os números complexos z = cos( 2θ) + i sen( θ) e w = cos(θ) + i sen(2θ), pode-se afirmar que
z =  .
.
A soma de todas as raízes reais da função ƒ(x) = cotg2 (x) - 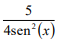 + 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
+ 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
A soma de todas as raízes reais da função ƒ(x) = cotg2 (x) - 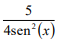 + 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
+ 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:


Analise as assertivas e assinale a alternativa que aponta a(s) correta(s).
I. sen π/6 = cos (π/2 - π/6)
II. cos 32100 = √3/2
III. tg π/6 = tg ( π/2 + π/6)
Analise as assertivas e assinale a alternativa que aponta a(s) correta(s).
I. sen π/6 = cos (π/2 - π/6)
II. cos 32100 = √3/2
III. tg π/6 = tg ( π/2 + π/6)
Para representar os harmônicos emitidos pelos sons
dos instrumentos da orquestra, usam-se funções
trigonométricas.
A expressão 2 sen2 x + 2 cos2 x – 5 envolve estas
funções e, para π < x < 3π/2, seu valor de é:
–3
A partir dessas informações, e sabendo que os ciclos da pressão arterial coincidem com os batimentos cardíacos, julgue o próximo item.
Na situação do gráfico em questão, a = 100 mmHg,
constante que mede o deslocamento do gráfico da função
Q(t) = bsen(ct + d) na direção do eixo vertical.
A partir dessas informações, e sabendo que os ciclos da pressão arterial coincidem com os batimentos cardíacos, julgue o próximo item.
Na situação do gráfico em questão, a = 100 mmHg,
constante que mede o deslocamento do gráfico da função
Q(t) = bsen(ct + d) na direção do eixo vertical.

Muitos diagnósticos em medicina são obtidos pela
monitoração de sinais vitais do paciente, como a pressão arterial, ou
seja, a pressão nas paredes dos vasos sanguíneos. Esse sinal é
exemplificado no gráfico acima, em que P(t) é a pressão, em
mmHg, e t é o tempo, em segundos. O gráfico mostra um
comportamento cíclico, corretamente descrito por uma função da
forma P(t) = a + bsen(ct + d), em que a, b, c e d são constantes
reais.
Assinale a alternativa correta:
A equação  tem duas raízes no intervalo
tem duas raízes no intervalo 
 para todo x pertencente ao intervalo
para todo x pertencente ao intervalo 

Se f e g são funções reais de variável real
definidas por f(x) = sen²x e g(x) = cos²x, então, seus
gráficos, construídos em um mesmo sistema de
coordenadas cartesianas, se cruzam exatamente nos
pontos cujas abcissas são
Considerando a função real de variável real
definida por f(x) = (cosx + secx + 2).cosx, onde x é
tal que cosx ≠ 0, é correto afirmar que a imagem de f
(isto é, o conjunto de valores de f) é
Em 2014 foi inaugurada a maior roda-gigante do
mundo, a High Roller, situada em Las Vegas. A figura
representa um esboço dessa roda-gigante, no qual o
ponto A representa uma de suas cadeiras:

A partir da posição indicada, em que o segmento OA
se encontra paralelo ao plano do solo, rotaciona-se a
High Roller no sentido anti-horário, em torno do ponto O.
Sejam t o ângulo determinado pelo segmento OA em
relação à sua posição inicial, e f a função que descreve
a altura do ponto A, em relação ao solo, em função de t.
Após duas voltas completas, f em o seguinte gráfico:

A expressão da função altura é dada por
Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:

A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t.
Após duas voltas completas, f em o seguinte gráfico:

A expressão da função altura é dada por
Uma pequena indústria produz ração para cachorro. A previsão da sua produção mês a mês para o ano de 2019, em quilogramas, é dada pela função
 ,
,
onde t representa o mês do ano, ou seja, t é um número natural tal que 1 ≤ t ≤ 12. Sendo assim, a maior e a menor produção prevista para o ano de 2019 se darão respectivamente nos meses:
Uma pequena indústria produz ração para cachorro. A previsão da sua produção mês a mês para o ano de 2019, em quilogramas, é dada pela função
 ,
,
onde t representa o mês do ano, ou seja, t é um número natural tal que 1 ≤ t ≤ 12. Sendo assim, a maior e a menor produção prevista para o ano de 2019 se darão respectivamente nos meses:
Uma característica bastante conhecida das funções trigonométricas seno, cosseno e
tangente é sua periodicidade. O período da função real ƒ(x) = cos(4x - π) é
Parte do gráfico da função ƒ(x) = 1 + 2. sen(2x) está representado na Figura abaixo.
O conjunto imagem Im(ƒ) e o período p dessa
função são:


Em estudo divulgado recentemente na The Optical Society of
America, pesquisadores da Tong University revelaram uma
forma de transmitir dados de comunicação de forma segura
utilizando as águas dos mares como meio de transporte das
informações. No artigo, os cientistas apresentam o seguinte
gráfico como parte dos resultados.

Uma função trigonométrica que modela razoavelmente bem
a curva indicada por A no gráfico do artigo, com x em graus e
y em “coincidências em 1 s”, é
Em estudo divulgado recentemente na The Optical Society of America, pesquisadores da Tong University revelaram uma forma de transmitir dados de comunicação de forma segura utilizando as águas dos mares como meio de transporte das informações. No artigo, os cientistas apresentam o seguinte gráfico como parte dos resultados.

Uma função trigonométrica que modela razoavelmente bem
a curva indicada por A no gráfico do artigo, com x em graus e
y em “coincidências em 1 s”, é
A figura 1 indica o gráfico da função trigonométrica, de  em
em
 , definida por y = sen x. Seu gráfico foi desenhado no plano
cartesiano de eixos ortogonais paralelos aos lados do retângulo
PQRS e origem no centro desse retângulo. Sabe-se, ainda,
que de A até B ocorre um período completo da senoide.
, definida por y = sen x. Seu gráfico foi desenhado no plano
cartesiano de eixos ortogonais paralelos aos lados do retângulo
PQRS e origem no centro desse retângulo. Sabe-se, ainda,
que de A até B ocorre um período completo da senoide.

Em seguida, o retângulo PQRS é enrolado perfeitamente,
formando um cilindro circular reto, como se vê na figura 2.
A senoide da figura 1 origina uma elipse sobre a superfície
lateral do cilindro, como indicado na figura 2.

O comprimento do eixo maior da elipse que foi produzida sobre
a superfície do cilindro, na unidade de medida de comprimento
dos eixos cartesianos, é igual a:
 em
em
 , definida por y = sen x. Seu gráfico foi desenhado no plano
cartesiano de eixos ortogonais paralelos aos lados do retângulo
PQRS e origem no centro desse retângulo. Sabe-se, ainda,
que de A até B ocorre um período completo da senoide.
, definida por y = sen x. Seu gráfico foi desenhado no plano
cartesiano de eixos ortogonais paralelos aos lados do retângulo
PQRS e origem no centro desse retângulo. Sabe-se, ainda,
que de A até B ocorre um período completo da senoide.

Uma pessoa usa um programa de computador que
descreve o desenho da onda sonora correspondente a um
som escolhido. A equação da onda é dada, num sistema
de coordenadas cartesianas, por y = a . sen[b(x + c)],
em que os parâmetros a, b, c são positivos. O programa
permite ao usuário provocar mudanças no som, ao fazer
alterações nos valores desses parâmetros. A pessoa
deseja tornar o som mais agudo e, para isso, deve diminuir
o período da onda.
O(s) único(s) parâmetro(s) que necessita(m) ser
alterado(s) é(são)
Sejam f, g: R → R funções definidas por f(x) = sen x, g(x) = sen 2x e P(a,b) um ponto na interseção dos gráficos de f e g. Os possíveis valores para tg2 a são
Um técnico precisa consertar o termostato do aparelho
de ar-condicionado de um escritório, que está desregulado.
A temperatura T, em graus Celsius, no escritório, varia de
acordo com a função T (h) = A + B sen ,
sendo h o tempo, medido em horas, a partir da meia-noite
(0 ≤ h ≤ 24) e A e B os parâmetros que o técnico precisa
regular. Os funcionários do escritório pediram que a
temperatura máxima fosse 26°C, a mínima 18°C, e
que durante a tarde a temperatura fosse menor do que
durante a manhã.
,
sendo h o tempo, medido em horas, a partir da meia-noite
(0 ≤ h ≤ 24) e A e B os parâmetros que o técnico precisa
regular. Os funcionários do escritório pediram que a
temperatura máxima fosse 26°C, a mínima 18°C, e
que durante a tarde a temperatura fosse menor do que
durante a manhã.
Quais devem ser os valores de A e de B para que o pedido
dos funcionários seja atendido?
Um técnico precisa consertar o termostato do aparelho
de ar-condicionado de um escritório, que está desregulado.
A temperatura T, em graus Celsius, no escritório, varia de
acordo com a função T (h) = A + B sen ,
sendo h o tempo, medido em horas, a partir da meia-noite
(0 ≤ h ≤ 24) e A e B os parâmetros que o técnico precisa
regular. Os funcionários do escritório pediram que a
temperatura máxima fosse 26°C, a mínima 18°C, e
que durante a tarde a temperatura fosse menor do que
durante a manhã.
,
sendo h o tempo, medido em horas, a partir da meia-noite
(0 ≤ h ≤ 24) e A e B os parâmetros que o técnico precisa
regular. Os funcionários do escritório pediram que a
temperatura máxima fosse 26°C, a mínima 18°C, e
que durante a tarde a temperatura fosse menor do que
durante a manhã.
Quais devem ser os valores de A e de B para que o pedido dos funcionários seja atendido?
Para se trabalhar com a “escala inimaginável de tempo” mencionada no último parágrafo do texto, poderia ser feita uma transformação que associa cada número da escala a um bem menor, de modo que a quantidade de zeros fosse drasticamente reduzida. Por exemplo, o número 10100 (1 seguido de 100 zeros) pode ser associado ao número 100. A função matemática que tem essa propriedade é a


Considerando o texto acima, julgue o item e assinale a
opção correta.