a2a64865-e8
FAME 2014 - Matemática - Cone, Geometria Espacial, Cilindro
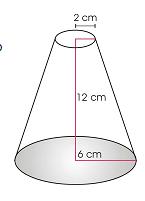
O pluviômetro é um aparelho utilizado para medir a quantidade de precipitação de chuva por unidade de área, durante certo intervalo de tempo.
A medida é sempre expressa em milímetros de altura ou litros por metro quadrado.
Na figura, tem-se o exemplo de um pluviômetro muito utilizado. Nesse funil, a área onde a água da chuva é captada tem formato circular e ele é encaixado em um cilindro circular reto onde a água captada é depositada.

Suponhamos que, em um dia chuvoso, a precipitação medida no pluviômetro tenha sido de 2,8 cm no cilindro.
Sabendo que o raio da circunferência do funil é o dobro do raio da base do cilindro cuja área mede 25  cm2 , qual a medida do volume de chuva, em litros, precipitado em cada metro quadrado da região aonde foi coletada a medida do pluviômetro?
cm2 , qual a medida do volume de chuva, em litros, precipitado em cada metro quadrado da região aonde foi coletada a medida do pluviômetro?
O pluviômetro é um aparelho utilizado para medir a quantidade de precipitação de chuva por unidade de área, durante certo intervalo de tempo.
A medida é sempre expressa em milímetros de altura ou litros por metro quadrado.
Na figura, tem-se o exemplo de um pluviômetro muito utilizado. Nesse funil, a área onde a água da chuva é captada tem formato circular e ele é encaixado em um cilindro circular reto onde a água captada é depositada.

Suponhamos que, em um dia chuvoso, a precipitação medida no pluviômetro tenha sido de 2,8 cm no cilindro.
Sabendo que o raio da circunferência do funil é o dobro do raio da base do cilindro cuja área mede 25 cm2 , qual a medida do volume de chuva, em litros, precipitado em cada metro quadrado da região aonde foi coletada a medida do pluviômetro?
cm2 , qual a medida do volume de chuva, em litros, precipitado em cada metro quadrado da região aonde foi coletada a medida do pluviômetro?
A medida é sempre expressa em milímetros de altura ou litros por metro quadrado.
Na figura, tem-se o exemplo de um pluviômetro muito utilizado. Nesse funil, a área onde a água da chuva é captada tem formato circular e ele é encaixado em um cilindro circular reto onde a água captada é depositada.

Suponhamos que, em um dia chuvoso, a precipitação medida no pluviômetro tenha sido de 2,8 cm no cilindro.
Sabendo que o raio da circunferência do funil é o dobro do raio da base do cilindro cuja área mede 25
 cm2 , qual a medida do volume de chuva, em litros, precipitado em cada metro quadrado da região aonde foi coletada a medida do pluviômetro?
cm2 , qual a medida do volume de chuva, em litros, precipitado em cada metro quadrado da região aonde foi coletada a medida do pluviômetro?A
7.
B
14.
C
21.
D
28.








 Com base nessas informações e considerando o texto I, julgue os itens 38 e 39 e assinale a opção correta no item 40, que é do tipo C.
Com base nessas informações e considerando o texto I, julgue os itens 38 e 39 e assinale a opção correta no item 40, que é do tipo C.



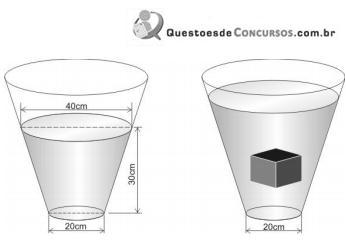
 do volume de água já existente no recipiente.
do volume de água já existente no recipiente.  =3 )
=3 )