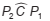6ac815d9-e9
UERJ 2021 - Matemática - Áreas e Perímetros, Circunferências e Círculos, Geometria Plana
A figura a seguir representa uma circunferência de centro O e raio 1. Considere AC, BD e PQ
diâmetros, com AC e BD perpendiculares. Observe-se ainda, que o ponto P pertence ao arco e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP.
e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP.

Sabendo que sen 2α = 2 senα . cosα, a área do triângulo PQR é igual a:
A figura a seguir representa uma circunferência de centro O e raio 1. Considere AC, BD e PQ
diâmetros, com AC e BD perpendiculares. Observe-se ainda, que o ponto P pertence ao arco e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP.
e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP.
 e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP.
e o ponto R, ao raio OD; o segmento QR é paralelo a AC; e α é a medida do ângulo CÔP. 
Sabendo que sen 2α = 2 senα . cosα, a área do triângulo PQR é igual a:
A

B

C
sen 2α
D
cos 2α
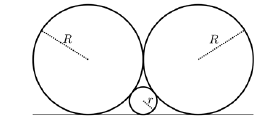



 em cm, é
em cm, é