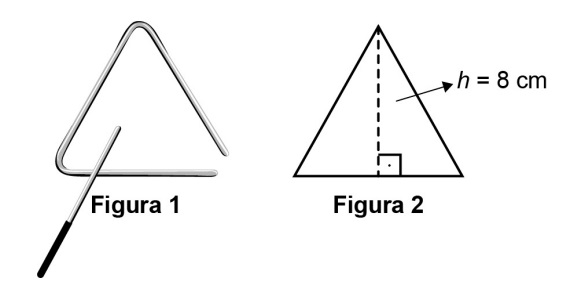
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.

Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de
diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além
disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das
circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?