Questõessobre Estática - Momento da Força/Equilíbrio e Alavancas

InícioTodas as questões
1
1
Foram encontradas 115 questões
f365049b-af
UNIOESTE 2017 - Física - Estática e Hidrostática, Dinâmica, Leis de Newton, Estática - Momento da Força/Equilíbrio e Alavancas

Um semáforo, em equilíbrio estático, está instalado em uma via urbana, e é sustentado por uma haste horizontal fixa em um poste vertical e por um cabo com inclinação de 30º conforme a figura abaixo. Em relação à distribuição e intensidade das forças que atuam no ponto X, é CORRETO afirmar:

A
o semáforo é mantido em equilíbrio devido à atuação exclusiva de duas forças no ponto X: uma força vertical representada pelo vetor força peso do semáforo e outra de tração orientada ao longo do cabo.
B
a força peso e a componente vertical da força de tração orientada ao longo do cabo formam um par açãoreação conforme a terceira Lei de Newton.
C
para o sistema da figura, o aumento do ângulo entre o cabo e a haste horizontal de 30º para 40º gera acréscimo na intensidade da componente vertical da força de tração com o consequente aumento na força peso do semáforo.
D
em relação a um eixo horizontal paralelo à haste e que passa pelo ponto X, o somatório das forças é diferente de zero, pois atua somente a componente horizontal da força de tração responsável por manter o semáforo fixo à haste horizontal.
E
no sistema mostrado na figura, as componentes das forças que atuam em relação a um eixo horizontal que passa pelo ponto X têm soma igual a zero, assim como as componentes das forças que atuam em relação a um eixo vertical que passa pelo ponto X.
f368e4c9-af
UNIOESTE 2017 - Física - Estática e Hidrostática, Dinâmica, Leis de Newton, Estática - Momento da Força/Equilíbrio e Alavancas

Uma pessoa usa uma chave de boca para apertar um parafuso, conforme a figura abaixo. A distância do centro do parafuso até a extremidade do cabo da chave de boca é de 30 cm e a força F, vertical, aplicada a 5 cm da extremidade do cabo da chave, possui intensidade F = 20 N. Assinale a alternativa CORRETA.

A
O torque gerado por F tem módulo igual a 2,5√2 N.m e orientação paralela à F.
B
O torque gerado por F atua ao longo do eixo do parafuso, sendo sua orientação perpendicular à F e ao plano da página.
C
A orientação da força F representada na figura é aquela que fornece a situação de torque máximo, pois o ângulo entre o torque e o vetor força F é de 90º.
D
Na situação apresentada na figura, a componente de F paralela ao eixo do cabo da chave é nula, por esse motivo essa componente não gera torque.
E
Após uma rotação no parafuso em 45º no sentido horário, de forma que o cabo da chave de boca esteja na posição horizontal e mantendo F na vertical, o torque terá módulo nulo.
4af9c45b-0a
ENEM 2019 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Slackline é um esporte no qual o atleta deve se equilibrar e executar manobras estando sobre uma fita esticada. Para a prática do esporte, as duas extremidades da fita são fixadas de forma que ela fique a alguns centímetros do solo. Quando uma atleta de massa igual a 80 kg está exatamente no meio da fita, essa se desloca verticalmente, formando um ângulo de 10° com a horizontal, como esquematizado na figura. Sabe-se que a aceleração da gravidade é igual a 10 m s−2, cos(10°) = 0,98 e sen(10°) = 0,17.



Qual é a força que a fita exerce em cada uma das árvores por causa da presença da atleta?

A
4,0 × 102 N
B
4,1 × 102 N
C
8,0 × 102 N
D
2,4 × 103 N
E
4,7 × 103 N
db25e764-8c
UERJ 2019 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Um portão fixado a uma coluna está articulado nos pontos P1 e P2, conforme ilustra a imagem a seguir, que indica também três outros pontos: O, A e B. Sabe-se que = 2,4 m e = 0,8 m.

Para abrir o portão, uma pessoa exerce uma força perpendicular de 20 N no ponto B, produzindo um momento resultante MB.

O menor valor da força que deve ser aplicada no ponto A para que o momento resultante seja igual a MB, em newtons, corresponde a:

A
15
B
30
C
45
D
60
d401b9da-3f
UEL 2018 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Na figura 2, é possível observar esculturas construídas com a sobreposição de pedras. Com base nos conhecimentos sobre equilíbrio e estática, é correto afirmar que cada uma das esculturas está em equilíbrio estático

Observe a figura 2 a seguir e responda à questão.


                             

A
instável, pois o momento de força atuante na pedra superior varia com o tempo.
B
estável, pois a resultante das forças que atuam sobre a última pedra é positiva.
C
instável, pois a resultante das forças que atuam sobre o conjunto das pedras é nula.
D
estável, pois a resultante das forças que atuam sobre a primeira pedra é positiva.
E
instável, pois a resultante das forças que atuam sobre o conjunto das pedras é negativa.
0e704d7b-4e
ENEM 2013 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Retirar a roda de um carro é uma tarefa facilitada por algumas características da ferramenta utilizada, habitualmente denominada chave de roda. As figuras representam alguns modelos de chaves de roda:



Em condições usuais, qual desses modelos permite a retirada da roda com mais facilidade?

A
1, em função de o momento da força ser menor.
B
1, em função da ação de um binário de forças.
C
2, em função de o braço da força aplicada ser maior.
D
3, em função de o braço da força aplicada poder variar.
E
3, em função de o momento da força produzida ser maior.
e339c3fd-38
UNICAMP 2017 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

A figura abaixo ilustra uma alavanca que gira em torno do ponto O. Dois triângulos, do mesmo material e de mesma espessura, estão presos por fios de massa desprezível nos extremos da alavanca. Um triângulo é equilátero; o outro é retângulo e isósceles, e sua hipotenusa tem o mesmo comprimento que os lados do triângulo equilátero. Note que, neste caso, o peso dos objetos é proporcional à sua área. Conclui-se que, na condição de equilíbrio da alavanca, a razão das distâncias, i/e, é igual a


Sempre que necessário, use aceleração da gravidade g = 10 m/s2 .

A
√3.
B
√3/3.
C
2.
D
3.
8212abae-e5
UECE 2017 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Uma chaminé de 30 m de altura pende, sem se quebrar, até uma inclinação de 30° com a vertical. Considere a aceleração da gravidade como 10 m/s2 e o diâmetro da chaminé muito menor que sua altura. Suponha que nessa configuração haja uma força vertical de 1 N puxando rumo ao solo a ponta da chaminé. Nesta situação, o torque exercido por essa força no topo da chaminé vale, em N×m,

A
150.
B
30√2.
C
300√2.
D
15.
d40de7d2-9c
UERJ 2017, UERJ 2017, UERJ 2017 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Uma luminária com peso de 76 N está suspensa por um aro e por dois fios ideais. No esquema, as retas AB e BC representam os fios, cada um medindo 3 m, e D corresponde ao ponto médio entre A e C.



Sendo BD = 1,2 m e A, C e D pontos situados na mesma horizontal, a tração no fio AB, em newtons, equivale a:

A
47,5
B
68,0
C
95,0
D
102,5
eb349a36-6e
UERJ 2012 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Um homem de massa igual a 80 kg está em repouso e em equilíbrio sobre uma prancha rígida de 2,0 m de comprimento, cuja massa é muito menor que a do homem.

A prancha está posicionada horizontalmente sobre dois apoios, A e B, em suas extremidades, e o homem está a 0,2 m da extremidade apoiada em A.

A intensidade da força, em newtons, que a prancha exerce sobre o apoio A equivale a:

A
200
B
360
C
400
D
720
34facd22-3b
UFPR 2016 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Uma mola de massa desprezível foi presa a uma estrutura por meio da corda “b”. Um corpo de massa “m” igual a 2000 g está suspenso por meio das cordas “a”, “c” e “d”, de acordo com a figura ao lado, a qual representa a configuração do sistema após ser atingido o equilíbrio. Considerando que a constante elástica da mola é 20 N/cm e a aceleração gravitacional é 10 m/s2 , assinale a alternativa que apresenta a deformação que a mola sofreu por ação das forças que sobre ela atuaram, em relação à situação em que nenhuma força estivesse atuando sobre ela. Considere ainda que as massas de todas as cordas e da mola são irrelevantes. 

A
0,5 cm.
B
1,2 cm.
C
2,5 cm.
D
3,5 cm.
E
5,2 cm.
d147c8ed-e4
PUC-GO 2016 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Nos fragmentos do Texto 3 “Tentava acompanhar os passos de meu pai. [...] dizer-lhe que parasse.” Temos referência a movimento e a repouso. O movimento de um corpo pode ser de translação e/ou rotação. Para que um corpo permaneça em repouso, é necessário que esteja em equilíbrio de translação e rotação. Considere uma gangorra construída com uma tábua rígida, homogênea, de massa igual a 10 kg, com espessura e largura desprezíveis em relação a seu comprimento, que é de 8 m. A tábua pode girar em torno de um eixo de rotação colocado perpendicularmente ao seu comprimento, a 4 m de cada uma das extremidades. Duas pessoas, uma de massa m1 = 85 kg e outra de massa m2 = 40 kg, estão sentadas em cada uma das extremidades da tábua. Para que a tábua fique em equilíbrio horizontal, uma terceira pessoa é colocada entre o eixo de rotação e a pessoa mais leve, a uma distância de 1,5 m desse eixo. A massa da terceira pessoa é de (assinale a resposta correta):

TEXTO 3

                          Escalada para o inferno

Iniciava-se ali, meu estágio no inferno. A ardida solidão corroía cada passo que eu dava. Via crucis vivida aos seis anos de idade, ao sol das duas horas. Vermelhidão por todos os lados daquela rua íngreme e poeirenta. Meus olhos pediam socorro mas só encontravam uma infinitude de terra e desolação. Tentava acompanhar os passos de meu pai. E eles eram enormes. Não só os passos mas as pernas. Meus olhos olhavam duplamente: para os passos e para as pernas e não alcançavam nem um nem outro. Apenas se defrontavam com um vazio empoeirado que entrava no meu ser inteiro. Eu queria chorar mas tinha medo. Tropeçava a cada tentativa de correr para alcançar meu pai. E eu tinha medo de ter medo. E eu tinha medo de chorar. E era um sofrimento com todos os vórtices de agonia. À minha frente, até onde meus olhos conseguiram enxergar, estavam os pés e as pernas de meu pai que iam firmes subindo subindo subindo sem cessar. À minha volta eu podia ver e sentir a terra vermelha e minha vida envolta num turbilhão de desespero. Na verdade eu não sabia muito bem para onde estava indo. Eu era bestializado nos meus próprios passos. Nas minhas próprias pernas. Tinha a impressão que o ponto de chegada era aquele redemoinho em que me encontrava e que dele nunca mais sairia. Na ânsia de ir sem querer ir eu gaguejava no caminhar. E olhava com sofreguidão para os meus pés e via ainda com mais aflição que os bicos de meus sapatos novos estavam sujos daquela poeira impregnante, vasculhante, suja. Eu sempre gostei de sapatos. Eu sempre gostei de sapatos novos. Novos e luzidios. E eles estavam sujos. Cobertos de poeira. E a subida prosseguia inalterada. Tentava olhar para o alto e só conseguia ver os enormes joelhos de meu pai que dobravam num ritmo compassado. Via suas pernas e seus pés. E só. Sentia, lá no fundo, um desejo calado de dizer alguma coisa. De dizer-lhe que parasse. Que fosse mais devagar. Que me amparasse. Mas esse desejo era um calo na minha pequenina garganta que jamais seria curado. E eu prossegui ao extremo de meus limites. Tinha de acontecer: desamarrou o cadarço de meu sapato. A loucura do sol das duas horas parece ter se engraçado pelo meu desatino. Tudo ficou muito mais quente. Tudo ficou mais empoeirado e muito mais vermelho. O desatino me levou ao choro. Não sei se chorei ou se choraminguei. Só sei que dei índices de que eu precisava de meu pai. E ele atendeu. Voltou-se para mim e viu que estava pisando no cadarço. Que estava prestes a cair. Então me socorreu. Olhou-me nos olhos com a expressão casmurra. Levou suas enormes mãos aos meus pés e amarrou o cadarço firmemente com um intrincado nó. A cena me levou a um estado de cegueira anestésica tão intensa que sofri uma espécie de amnésia passageira. Estado de torpor. Quando dei por mim, já tinha chegado ao meu destino: cadeira do barbeiro. Alta, prepotente e giratória. Ele, o barbeiro, cabeça enorme, mãos enormes, enormes unhas, sorriso nos lábios dos quais surgiam grandes caninos. Ele portava enorme máquina que apontava em minha direção. E ouvi a voz do pai: pode tirar quase tudo! deixa só um pouco em cima! Ali, finalmente, para lembrar Rimbaud, ia se encerrar meu estágio no inferno.

(GONÇALVES, Aguinaldo. Das estampas. São Paulo: Nankin, 2013. p. 45-46.)

A
45 kg.
B
72 kg.
C
98 kg
D
120 kg.
598f2542-d6
PUC - RS 2016 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

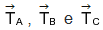No sistema apresentado na figura abaixo, o bloco M está em equilíbrio mecânico em relação a um referencial inercial. Os três cabos, A, B e C, estão submetidos, cada um, a tensões respectivamente iguais a https://qcon-assets-production.s3.amazonaws.com/images/provas/52206/oi.png . Qual das alternativas abaixo representa corretamente a relação entre os módulos dessas forças tensoras?

A
TA > TC
B
TA < TC
C
TA = TC
D
TB = TC
E
TB > TC
420184b3-be
ENEM 2016 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

A figura mostra uma balança de braços iguais, em equilíbrio, na Terra, onde foi colocada uma massa m, e a indicação de uma balança de força na Lua, onde a aceleração da gravidade é igual a 1,6 m/s2, sobre a qual foi colocada uma massa M.

A razão das massas M/m é

A
4,0.
B
2,5.
C
0,4.
D
1 ,0.
E
0,25.
3ee74a30-91
UECE 2015 - Física - MCU - Movimento Circular Uniforme, Estática e Hidrostática, Dinâmica, Leis de Newton, Cinemática, Estática - Momento da Força/Equilíbrio e Alavancas

Um ventilador de teto gira a uma velocidade angular de 420 rpm, tem 130 W de potência e hélice com 96 cm de diâmetro. Devido à força de atrito com o ar, há forças atuando ao longo de cada uma das hélices. Essas forças atuam em pontos localizados desde próximos ao eixo de rotação a pontos na extremidade da hélice, provocando torques diferentes em relação ao eixo de rotação. Considerando que a força de atrito em cada ponto seja proporcional à velocidade linear do ponto, é correto afirmar que esse torque, a uma distância R do eixo de rotação, é proporcional a

A
R 2 .
B
R.
C
R 3 .
D
R 4 .
bd936662-31
UERJ 2016, UERJ 2016 - Física - Estática - Momento da Força/Equilíbrio e Alavancas

Um sistema é constituído por seis moedas idênticas fixadas sobre uma régua de massa desprezível que está apoiada na superfície horizontal de uma mesa, conforme ilustrado abaixo. Observe que, na régua, estão marcados pontos equidistantes, numerados de 0 a 6.
Ao se deslocar a régua da esquerda para a direita, o sistema permanecerá em equilíbrio na horizontal até que determinado ponto da régua atinja a extremidade da mesa.

De acordo com a ilustração, esse ponto está representado pelo seguinte número:

A
4
B
3
C
2
D
1
d4868622-96
CEDERJ 2013 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Um trabalhador deseja deslocar uma pedra com o auxílio de uma alavanca. Ele tem a possibilidade de colocar o ponto de apoio, mediante o uso de cunhas, nas posições 1 ou 2, como ilustrado nas figuras. Considere que o trabalhador exercerá uma força na direção perpendicular à haste e que ele tem as alternativas de exercê-la nos pontos 1, 2, 3 ou 4.

                                    

Dentre as alternativas, assinale aquela que permite ao trabalhador deslocar a pedra com menos esforço.

A
Posição do apoio 1 

Ponto de aplicação da força 4
B
Posição do apoio 1 

Ponto de aplicação da força 2
C
Posição do apoio 2   

Ponto de aplicação da força 4 
D
Posição do apoio 2 

Ponto de aplicação da força 3
d08725af-94
UERJ 2013 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

A figura abaixo ilustra uma ferramenta utilizada para apertar ou desapertar determinadas peças metálicas. 

                                     

Para apertar uma peça, aplicando-se a menor intensidade de força possível, essa ferramenta deve ser segurada de acordo com o esquema indicado em:


A



B



C



D



3d7a56da-8d
UNESP 2011 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

Um lustre está pendurado no teto de uma sala por meio de dois fios inextensíveis, de mesmo comprimento e de massas desprezíveis, como mostra a figura 1, onde o ângulo que cada fio faz com a vertical é 30° . As forças de tensão nos fios têm a mesma intensidade.

                         

Considerando cos 30º ≅ 0,87, se a posição do lustre for modificada e os fios forem presos ao teto mais distantes um do outro, de forma que o ângulo que cada um faz com a vertical passe a ser o dobro do original, como mostra a figura 2, a tensão em cada fio será igual a


A
0,50 do valor original.
B
1,74 do valor original.
C
0,86 do valor original.
D
2,00 do valor original.
E
3,46 do valor original.
955eabfd-7f
ENEM 2015 - Física - Estática e Hidrostática, Estática - Momento da Força/Equilíbrio e Alavancas

   Em um experimento, um professor levou para a sala de aula um saco de arroz, um pedaço de madeira triangular e uma barra de ferro cilíndrica e homogênea. Ele propôs que fizessem a medição da massa da barra utilizando esses objetos. Para isso, os alunos fizeram marcações na barra, dividindo-a em oito partes iguais, e em seguida apoiaram-na sobre a base triangular, com o saco de arroz pendurado em uma de suas extremidades, até atingir a situação de equilíbrio.




Nessa situação, qual foi a massa da barra obtida pelos alunos?


A
3.00 kg
B
3,75 kg
C
5.00 kg
D
6.00 kg
E
15.00 kg