Para alcançar o teto de uma garagem, uma pessoa sobe em
uma escada AB e fica parada na posição indicada na figura 1.
A escada é mantida em repouso, presa por cordas horizontais, e apoiada no chão. Na figura 2 estão indicadas algumas
distâncias e desenhadas algumas forças que atuam sobre a
escada nessa situação: seu peso PE = 300 N, a força aplicada pelo homem sobre a escada FH = 560 N e a tração aplicada pelas cordas,  . A força de contato com o solo, aplicada no
ponto B, não está indicada nessa figura.
. A força de contato com o solo, aplicada no
ponto B, não está indicada nessa figura.

Considerando um eixo passando pelo ponto B, perpendicular
ao plano que contém a figura 2, para o cálculo dos momentos
aplicados pelas forças sobre a escada, a intensidade da força
de tração  é
é
Para alcançar o teto de uma garagem, uma pessoa sobe em
uma escada AB e fica parada na posição indicada na figura 1.
A escada é mantida em repouso, presa por cordas horizontais, e apoiada no chão. Na figura 2 estão indicadas algumas
distâncias e desenhadas algumas forças que atuam sobre a
escada nessa situação: seu peso PE = 300 N, a força aplicada pelo homem sobre a escada FH = 560 N e a tração aplicada pelas cordas,  . A força de contato com o solo, aplicada no
ponto B, não está indicada nessa figura.
. A força de contato com o solo, aplicada no
ponto B, não está indicada nessa figura.

Considerando um eixo passando pelo ponto B, perpendicular
ao plano que contém a figura 2, para o cálculo dos momentos
aplicados pelas forças sobre a escada, a intensidade da força
de tração  é
é

 será
será
 de módulo igual a 1 m/s. Desprezando os atritos e
sendo Eꞌ
de módulo igual a 1 m/s. Desprezando os atritos e
sendo Eꞌ é igual a
é igual a
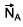 e, sobre a caixa B, uma força
e, sobre a caixa B, uma força 

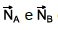 e as distâncias x e y,
tal que
e as distâncias x e y,
tal que 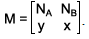 Sendo M
Sendo M sendo β dado em decibels (dB) e
I
sendo β dado em decibels (dB) e
I


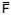 , sendo aplicada à caixa paralelamente
à superfície inclinada, como mostra a figura 2.
, sendo aplicada à caixa paralelamente
à superfície inclinada, como mostra a figura 2.
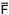 é 200 N. Se o ângulo
for aumentado para um valor θ
é 200 N. Se o ângulo
for aumentado para um valor θ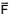 passa
a ser de
passa
a ser de









