Questõesde USP sobre Matemática
A dona de uma lanchonete observou que, vendendo um
combo a R$ 10,00, 200 deles são vendidos por dia, e que, para
cada redução de R$ 1,00 nesse preço, ela vende 100 combos
a mais. Nessas condições, qual é a máxima arrecadação diária
que ela espera obter com a venda desse combo?
A menor esfera na qual um paralelepípedo reto‐retângulo de
medidas 7 cm × 4 cm × 4 cm está inscrito tem diâmetro de
Um objeto é formado por 4 hastes rígidas conectadas em seus
extremos por articulações, cujos centros são os vértices de um
paralelogramo. As hastes movimentam‐se de tal forma que o
paralelogramo permanece sempre no mesmo plano. A cada
configuração desse objeto, associa‐se θ, a medida do menor
ângulo interno do paralelogramo. A área da região delimitada
pelo paralelogramo quando θ = 90º é A.

Para que a área da região delimitada pelo paralelogramo seja A/2, o valor de θ é, necessariamente, igual a

O cilindro de papelão central de uma fita crepe tem raio
externo de 3 cm. A fita tem espessura de 0,01 cm e dá 100
voltas completas. Considerando que, a cada volta, o raio
externo do rolo é
aumentado no valor da
espessura da fita, o
comprimento total da fita
é de, aproximadamente,

Note e adote:
π ≡ 3,14.

Se, em 15 anos, o salário mínimo teve um aumento nominal
de 300% e a inflação foi de 100%, é correto afirmar que o
aumento real do salário mínimo, nesse período, foi de
Uma empresa estuda cobrir um vão entre dois prédios (com
formato de paralelepípedos reto‐retângulos) que têm paredes
laterais paralelas, instalando uma lona na forma de um
quadrilátero, com pontas presas nos pontos A, B, C e D,
conforme indicação da figura.
Sabendo que a lateral de um prédio tem 80 m de altura e 28 m
de largura, que a lateral do outro prédio tem 60 m de altura e
20 m de largura e que essas duas paredes laterais distam 15 m
uma da outra, a área total dessa lona seria de

Uma empresa estuda cobrir um vão entre dois prédios (com formato de paralelepípedos reto‐retângulos) que têm paredes laterais paralelas, instalando uma lona na forma de um quadrilátero, com pontas presas nos pontos A, B, C e D, conforme indicação da figura.
Sabendo que a lateral de um prédio tem 80 m de altura e 28 m de largura, que a lateral do outro prédio tem 60 m de altura e 20 m de largura e que essas duas paredes laterais distam 15 m uma da outra, a área total dessa lona seria de

Um triângulo retângulo com vértices denominados A,B e C apoia‐se sobre uma linha horizontal, que corresponde ao solo,
e gira sem escorregar no sentido horário. Isto é, se a posição
inicial é aquela mostrada na figura, o movimento começa com
uma rotação em torno do vértice C até o vértice A tocar o solo,
após o que passa a ser uma rotação em torno de A ,até o vértice B tocar o solo, e assim por diante.

Usando as dimensões indicadas na figura (AB = 1 e BC = 2),
qual é o comprimento da trajetória percorrida pelo vértice B,
desde a posição mostrada, até a aresta BC apoiar‐se no solo
novamente?
Um triângulo retângulo com vértices denominados A,B e C apoia‐se sobre uma linha horizontal, que corresponde ao solo, e gira sem escorregar no sentido horário. Isto é, se a posição inicial é aquela mostrada na figura, o movimento começa com uma rotação em torno do vértice C até o vértice A tocar o solo, após o que passa a ser uma rotação em torno de A ,até o vértice B tocar o solo, e assim por diante.

Usando as dimensões indicadas na figura (AB = 1 e BC = 2),
qual é o comprimento da trajetória percorrida pelo vértice B,
desde a posição mostrada, até a aresta BC apoiar‐se no solo
novamente?





Uma seta aponta para a posição zero no instante inicial. A cada
rodada, ela poderá ficar no mesmo lugar ou mover‐se uma
unidade para a direita ou mover‐se uma unidade para a
esquerda, cada uma dessas três possibilidades com igual
probabilidade.

Qual é a probabilidade de que, após 5 rodadas, a seta volte à
posição inicial?
Uma seta aponta para a posição zero no instante inicial. A cada rodada, ela poderá ficar no mesmo lugar ou mover‐se uma unidade para a direita ou mover‐se uma unidade para a esquerda, cada uma dessas três possibilidades com igual probabilidade.

Qual é a probabilidade de que, após 5 rodadas, a seta volte à
posição inicial?
O gráfico mostra a evolução diária, em certo intervalo de tempo
não especificado na abscissa, de dois índices econômicos,
normalizados para que suas médias, no mesmo período, sejam
ambas iguais a 1. O valor do índice 1 no dia i é xi e o valor do
índice 2 no dia i é yi.O gráfico ilustra como cada um dos índices
xi e yi varia em função de ݅i, mostrando os pontos (i, xi)(pontos escuros) e (i, yi) (pontos claros).

Para entender melhor a relação entre os dois índices, um novo
gráfico foi feito com os pares (xi ,yi) isto é, com o índice 1 na
abscissa contra o índice 2 na ordenada. O resultado foi:
O gráfico mostra a evolução diária, em certo intervalo de tempo não especificado na abscissa, de dois índices econômicos, normalizados para que suas médias, no mesmo período, sejam ambas iguais a 1. O valor do índice 1 no dia i é xi e o valor do índice 2 no dia i é yi.O gráfico ilustra como cada um dos índices xi e yi varia em função de ݅i, mostrando os pontos (i, xi)(pontos escuros) e (i, yi) (pontos claros).

Para entender melhor a relação entre os dois índices, um novo
gráfico foi feito com os pares (xi ,yi) isto é, com o índice 1 na
abscissa contra o índice 2 na ordenada. O resultado foi:





A figura mostra uma escada maciça de quatro degraus, todos
eles com formato de um paralelepípedo reto‐retângulo. A base
de cada degrau é um retângulo de dimensões 20 cm por 50 cm,
e a diferença de altura entre o piso e o primeiro degrau e entre
os degraus consecutivos é de 10 cm. Se essa escada for
prolongada para ter 20 degraus, mantendo o mesmo padrão,
seu volume será igual a

A figura mostra uma escada maciça de quatro degraus, todos eles com formato de um paralelepípedo reto‐retângulo. A base de cada degrau é um retângulo de dimensões 20 cm por 50 cm, e a diferença de altura entre o piso e o primeiro degrau e entre os degraus consecutivos é de 10 cm. Se essa escada for prolongada para ter 20 degraus, mantendo o mesmo padrão, seu volume será igual a

Forma‐se uma pilha de folhas de papel, em que cada folha tem
0,1 mm de espessura. A pilha é formada da seguinte maneira:
coloca‐se uma folha na primeira vez e, em cada uma das vezes
seguintes, tantas quantas já houverem sido colocadas
anteriormente. Depois de 33 dessas operações, a altura da
pilha terá a ordem de grandeza
Considere a função polinomial ƒ: ℝ → ℝ definida por
ƒ(x) : ax2 + bx + c
em que a , b, c ∈ ℝ e ܽa ≠ 0. No plano cartesiano xy ,a única
intersecção da reta y = 2 com o gráfico de ƒ é o ponto (2; 2) e
a intersecção da reta x = 0 com o gráfico de ƒ é o ponto
(0; -6). O valor de a + b + c é
Considere a função polinomial ƒ: ℝ → ℝ definida por
ƒ(x) : ax2 + bx + c
em que a , b, c ∈ ℝ e ܽa ≠ 0. No plano cartesiano xy ,a única intersecção da reta y = 2 com o gráfico de ƒ é o ponto (2; 2) e a intersecção da reta x = 0 com o gráfico de ƒ é o ponto (0; -6). O valor de a + b + c é
Um dono de restaurante assim descreveu a evolução do
faturamento quinzenal de seu negócio, ao longo dos dez
primeiros meses após a inauguração: “Até o final dos três
primeiros meses, tivemos uma velocidade de crescimento mais
ou menos constante, quando então sofremos uma queda
abrupta, com o faturamento caindo à metade do que tinha sido
atingido. Em seguida, voltamos a crescer, igualando, um mês e
meio depois dessa queda, o faturamento obtido ao final do
terceiro mês. Agora, ao final do décimo mês, estamos
estabilizando o faturamento em um patamar 50% acima do
faturamento obtido ao final do terceiro mês”.
Considerando que, na ordenada, o faturamento quinzenal está
representado emunidades desconhecidas, porém uniformemente
espaçadas, qual dos gráficos é compatível com a descrição do
comerciante?
Um dono de restaurante assim descreveu a evolução do faturamento quinzenal de seu negócio, ao longo dos dez primeiros meses após a inauguração: “Até o final dos três primeiros meses, tivemos uma velocidade de crescimento mais ou menos constante, quando então sofremos uma queda abrupta, com o faturamento caindo à metade do que tinha sido atingido. Em seguida, voltamos a crescer, igualando, um mês e meio depois dessa queda, o faturamento obtido ao final do terceiro mês. Agora, ao final do décimo mês, estamos estabilizando o faturamento em um patamar 50% acima do faturamento obtido ao final do terceiro mês”.
Considerando que, na ordenada, o faturamento quinzenal está representado emunidades desconhecidas, porém uniformemente espaçadas, qual dos gráficos é compatível com a descrição do comerciante?





Se a função ƒ:ℝ - {2} →ℝ é definida por ݂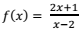 e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
Se a função ƒ:ℝ - {2} →ℝ é definida por ݂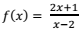 e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
e a
função ݃g : ℝ - {2} → ℝ é definida por ݃g(x) = ƒ(ƒ(x)), então
݃g(x) é igual a
Em uma família, o número de irmãs de cada filha é igual à
metade do número de irmãos. Cada filho tem o mesmo número
de irmãos e irmãs.
O número total de filhos e filhas da família é
Em uma família, o número de irmãs de cada filha é igual à metade do número de irmãos. Cada filho tem o mesmo número de irmãos e irmãs.
O número total de filhos e filhas da família é
Sejam Df e Dg os maiores subconjuntos de ℝ nos quais estão
definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g , respectivamente.
Nessas condições,
Sejam Df e Dg os maiores subconjuntos de ℝ nos quais estão definidas, respectivamente, as funções reais

Considere, ainda, If e Ig as imagens de f e de g , respectivamente.
Nessas condições,

Admitindo que a linha pontilhada represente o gráfico da
função ƒ(x) = sen(x) e que a linha contínua represente o
gráfico da função g(x)= αsen(βx) segue que

Admitindo que a linha pontilhada represente o gráfico da função ƒ(x) = sen(x) e que a linha contínua represente o gráfico da função g(x)= αsen(βx) segue que
Considere o polinômio
P(x) = xn + αn-1xn-1 +... + α1x + αo .
em que αo , ..., αn-1 ∈ ℝ. Sabe-se que as suas n raízes estão
sobre a circunferência unitária e que αo < 0.
O produto das n raízes de P(x), para qualquer inteiro n ≥ 1 , é:
Considere o polinômio
P(x) = xn + αn-1xn-1 +... + α1x + αo .
em que αo , ..., αn-1 ∈ ℝ. Sabe-se que as suas n raízes estão sobre a circunferência unitária e que αo < 0.
O produto das n raízes de P(x), para qualquer inteiro n ≥ 1 , é:
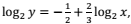 para x > 0, então
para x > 0, então 



