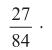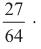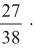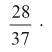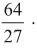d81e661c-28
UNIFESP 2005 - Matemática - Funções, Função de 1º Grau, Função de 2º Grau
Se A é o conjunto dos números reais diferentes de 1,

Se A é o conjunto dos números reais diferentes de 1,


A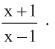
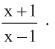
B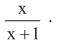
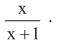
C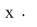
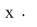
D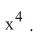
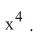
E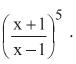
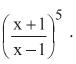

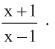
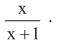
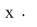
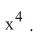
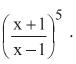


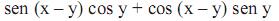 é equivalente a
é equivalente a , a área do triângulo de vértices A(0, 3), B(2, 0) e P é
, a área do triângulo de vértices A(0, 3), B(2, 0) e P é





 , é
, é




 tem vértice no ponto
tem vértice no ponto  O lugar geométrico dos vértices da parábola, quando t varia no conjunto dos números reais, é
O lugar geométrico dos vértices da parábola, quando t varia no conjunto dos números reais, é




 + ai, onde a é um número real positivo, representam no plano complexo vér- tices de um triângulo eqüilátero. Dado que
+ ai, onde a é um número real positivo, representam no plano complexo vér- tices de um triângulo eqüilátero. Dado que  o valor de a é:
o valor de a é: