Questõesde UNESP sobre Matemática

Segundo nutricionistas, uma refeição equilibrada, para uma pessoa adulta e saudável, não deve conter mais que 800 kcal. A tabela traz algumas opções de pedido, variedades dentro destas opções e o valor energético de cada uma delas.

Escolhendo-se um item de cada opção de pedido, a refeição de maior valor energético, que não exceda o limite de 800 kcal, será a composta de:

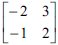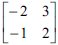Dada a matriz A = e definindo-se A0 = I, A1 = A e AK = A·A·A· …·A, com k fatores, onde I é uma matriz identidade de ordem 2, k ∈ IΝ e k ≥ 2, a matriz A15 será dada por:

Diferentes tipos de nanomateriais são descobertos a cada dia, viabilizando produtos mais eficientes, leves, adequados e, principalmente, de baixo custo.

São considerados nanomateriais aqueles cujas dimensões variam entre 1 e 100 nanômetros (nm), sendo que 1 nm equivale a 10–9 m, ou seja, um bilionésimo de metro.

Uma das características dos nanomateriais refere-se à relação entre seu volume e sua área superficial total.

Por exemplo, em uma esfera maciça de 1 cm de raio, a área superficial e o volume valem 4·π cm2 e (4/3)·π cm3, respectivamente. O conjunto de nanoesferas de 1 nm de raio, que possui o mesmo volume da esfera dada, tem a soma de suas áreas superficiais

No vazamento de petróleo da empresa americana Chevron do último dia 7 de novembro, na bacia de Campos/RJ, a mancha de óleo na superfície do mar assumiu grandes dimensões e teve seu pico de área entre os dias 12 e 14 daquele mês. O vazamento levou dias para ser contido, pois o petróleo continuava a escapar por fissuras, como mostrado na foto.

Dados 1 dm3 = 1 L e π ≈ 3 e sabendo que a altura média da lâmina de óleo sobre as águas era de 0,003 mm e que 1 barril de petróleo cru contém 160 litros de óleo, o número aproximado de barris que vazaram no incidente foi

O artigo Uma estrada, muitas florestas relata parte do trabalho de reflorestamento necessário após a construção do trecho sul do Rodoanel da cidade de São Paulo.

O engenheiro agrônomo Maycon de Oliveira mostra uma das árvores, um fumo-bravo, que ele e sua equipe plantaram em novembro de 2009. Nesse tempo, a árvore cresceu – está com quase 2,5 metros –, floresceu, frutificou e lançou sementes que germinaram e formaram descendentes [...] perto da árvore principal. O fumo-bravo [...] é uma espécie de árvore pioneira, que cresce rapidamente, fazendo sombra para as espécies de árvores de crescimento mais lento, mas de vida mais longa.

(Pesquisa FAPESP, janeiro de 2012. Adaptado.)

Considerando que a referida árvore foi plantada em 1.º de novembro de 2009 com uma altura de 1 dm e que em 31 de outubro de 2011 sua altura era de 2,5 m e admitindo ainda que suas alturas, ao final de cada ano de plantio, nesta fase de crescimento, formem uma progressão geométrica, a razão deste crescimento, no período de dois anos, foi de

O mercado automotivo na América Latina crescerá, no máximo, 2% em 2012. A estimativa é que, após esse período, ele voltará a expandir-se mais rapidamente, o que permitirá um crescimento médio de 5% nos próximos cinco anos.

afirmação foi feita pelo presidente da GM na América do Sul. Suas estimativas para as vendas, especificamente da GM na América Latina, são de 1,1 milhão de unidades em 2012 e de chegar a 1,4 milhão de veículos por ano até 2015.

(http://economia.estadao.com.br, 06.10.2011. Adaptado.)

A estimativa de que as vendas da GM, na América Latina, chegarão a 1,4 milhão de unidades no ano de 2015 pode ser considerada

Através dos gráficos das funções f(x) e g(x), os valores de f(g(0)) e g(f(1)) são, respectivamente:

Em um experimento sobre orientação e navegação de pombos,considerou-se o pombal como a origem O de um sistema de coordenadas cartesianas e os eixos orientados Sul-Norte (SN) e Oeste-Leste (WL). Algumas aves foram liberadas num ponto P que fica 52 km ao leste do eixo SN e a 30 km ao sul do eixo WL. O ângulo azimutal de P é o ângulo, em graus, medido no sentido horário a partir da semirreta ON até a semirreta OP. No experimento descrito, a distância do pombal até o ponto de liberação das aves, em km, e o ângulo azimutal, em graus, desse ponto são,respectivamente:

Dado: √3604 ≈ 60.

Em situação normal, observa-se que os sucessivos períodos de aspiração e expiração de ar dos pulmões em um indivíduo são iguais em tempo, bem como na quantidade de ar inalada e expelida.

A velocidade de aspiração e expiração de ar dos pulmões de um indivíduo está representada pela curva do gráfico, considerando apenas um ciclo do processo.

Sabendo-se que, em uma pessoa em estado de repouso, um ciclo de aspiração e expiração completo ocorre a cada 5 segundos e que a taxa máxima de inalação e exalação, em módulo, é 0,6 l/s, a expressão da função cujo gráfico mais se aproxima da curva representada na figura é:

O papelão utilizado na fabricação de caixas reforçadas é composto de três folhas de papel, coladas uma nas outras, sendo que as duas folhas das faces são “lisas” e a folha que se intercala entre elas é “sanfonada”, conforme mostrado na figura.

O fabricante desse papelão compra o papel em bobinas, de comprimento variável. Supondo que a folha “sanfonada” descreva uma curva composta por uma sequência de semicircunferências, com concavidades alternadas e de raio externo (RExt) de 1,5 mm, determine qual deve ser a quantidade de papel da bobina que gerará a folha “sanfonada”, com precisão de centímetros, para que, no processo de fabricação do papelão, esta se esgote no mesmo instante das outras duas bobinas de 102 m de comprimento de papel, que produzirão as faces “lisas”.

Dado: π ≈ 3,14.

Uma aeronave faz sua aproximação final do destino, quando seu comandante é informado pelo controlador de voo que, devido ao intenso tráfego aéreo, haverá um tempo de espera de 15 minutos para que o pouso seja autorizado e que ele deve permanecer em rota circular, em torno da torre de controle do aeroporto, a 1500 metros de altitude, até que a autorização para o pouso seja dada. O comandante, cônscio do tempo de espera a ser despendido e de que, nessas condições, a aeronave que pilota voa a uma velocidade constante de Vc (km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar.

Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.

No Brasil, desde junho de 2008, se for constatada uma concentração de álcool no sangue acima de 0,6 g/l, o motorista é detido e processado criminalmente.

(www.planalto.gov.br/ccivil_03/Ato2007-2010/2008/

Decreto/D6488.htm. Adaptado.)

Determine o número máximo de latas de cerveja que um motorista pode ingerir, antes de dirigir, para não ser processado criminalmente caso seja submetido ao teste.

Dados:

– o volume médio de sangue no corpo de um homem adulto é 7,0 litros;

– uma lata de cerveja de 350 ml contém 16 ml de álcool;

– 14% do volume de álcool ingerido por um homem adulto vão para a corrente sanguínea;

– a densidade do álcool contido em cervejas é de 0,8 g/ml.

Observação: Os resultados de todas as operações devem ser aproximados por duas casas decimais.

Observe o gráfico da função f(x) e analise as afirmações a seu respeito.

I. Se x1 , x2 ∈ Dom(f) e x2 > x1 , então f(x2 ) > f(x1 ).

II. Se x > 1, então f(x) < 0.

III. O ponto (2, –2) pertence ao gráfico de f(x).

IV. A lei de formação de f(x) representada no gráfico é dada por f(x) = - 1/2 ( x -1).

A alternativa que corresponde a todas as afirmações verdadeiras é: