Questõesde UNEB sobre Matemática
Para que o sistema linear 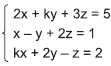 não tenha solução, o valor
da constante k deverá ser
não tenha solução, o valor
da constante k deverá ser
Para que o sistema linear 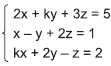 não tenha solução, o valor
da constante k deverá ser
não tenha solução, o valor
da constante k deverá ser
Se o polinômio p(x) satisfaz p(x).(4x2
+ kx + 1) = 8x5 − 32x3 − x2
+ 4,
em que k é uma constante, e duas de suas raízes são 2 e −2, então
sua terceira raiz estará no intervalo
O número de soluções da equação sen2x = senx, no intervalo
0 ≤ x < 2π é

Na figura, o círculo representa o tampo de uma mesa colocada em
um canto de uma sala, tocando duas paredes perpendiculares nos
pontos P e Q, respectivamente.
Sabendo-se que um ponto R, na borda da mesa, está a 10cm de uma
parede e a 20cm da outra, é correto afirmar que a região sombreada
entre o tampo e as duas paredes tem área, em cm2, igual a

Na figura, o círculo representa o tampo de uma mesa colocada em um canto de uma sala, tocando duas paredes perpendiculares nos pontos P e Q, respectivamente.
Sabendo-se que um ponto R, na borda da mesa, está a 10cm de uma
parede e a 20cm da outra, é correto afirmar que a região sombreada
entre o tampo e as duas paredes tem área, em cm2, igual a
Com a escassez de água, no planeta, a palavra de ordem é
economizar!
Pensando assim, um cidadão encheu um barril, depósito que estava
vazio, com 16 litros de água. Depois, equivocado, retirou 4 litros e os
substituiu por 4 litros de rum. Em seguida, retirou 4 litros da mistura
e os substituiu por outros 4 litros de rum. Repetiu a operação por outros
4 litros de rum, e continuou repetindo a operação uma 4ª vez, e seguiria
assim por diante.
Preocupado com o que estava fazendo, pensou em parar, pois, afinal,
na mistura, a parte de água que ainda restava, em litros, era de, apenas,
Uma empresa pode gastar, no máximo, R$15000,00 para comprar 400
unidades de certo material. De determinada marca, o material custa
R$25,00 por unidade, e de outra, de melhor qualidade, custa R$45,00
por unidade.
Efetuada a compra, tem-se que a razão entre o número de unidades
compradas da melhor marca e o da marca inferior deve ser, no
máximo,
Na revisão do texto, contido em 10 páginas de um trabalho escolar, foram identificados erros
de digitação, de acordo com a tabela

A variância do número de erros é igual a
Na revisão do texto, contido em 10 páginas de um trabalho escolar, foram identificados erros de digitação, de acordo com a tabela

A variância do número de erros é igual a

De um cubo maciço de aresta x, retiram-se três blocos — dois prismas retos de base triangular
e um paralelepípedo reto — obtendo-se um sólido em forma de U, de volume V = kx3 u.v., k∈R,
representado na figura.
O valor de k é

De um cubo maciço de aresta x, retiram-se três blocos — dois prismas retos de base triangular e um paralelepípedo reto — obtendo-se um sólido em forma de U, de volume V = kx3 u.v., k∈R, representado na figura.
O valor de k é
Sobre a reta s de equação y − 2x − 1= 0 e a circunferência C de equação x2 + y2 − 2x + y − 1= 0,
afirma-se:
I. C tem centro no ponto O = (1, -1/2).
II. s é tangente a C.
III. s determina com o eixo das abscissas um ângulo θ tal que senθ = 2√5/5 .
Para essas afirmações, pode-se garantir que é verdadeira a alternativa
Sobre a reta s de equação y − 2x − 1= 0 e a circunferência C de equação x2 + y2 − 2x + y − 1= 0, afirma-se:
I. C tem centro no ponto O = (1, -1/2).
II. s é tangente a C.
III. s determina com o eixo das abscissas um ângulo θ tal que senθ = 2√5/5 .
Para essas afirmações, pode-se garantir que é verdadeira a alternativa
Em uma aula de exercícios, um professor de Matemática propôs aos seus alunos a construção
do gráfico da função real definida por 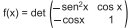 , 0 ≤ x ≤ π.
, 0 ≤ x ≤ π.
Cinco gráficos distintos, dados a seguir, foram esboçados pelos alunos.
Dentre eles, o que melhor representa a função f é
Em uma aula de exercícios, um professor de Matemática propôs aos seus alunos a construção
do gráfico da função real definida por 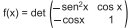 , 0 ≤ x ≤ π.
, 0 ≤ x ≤ π.
Cinco gráficos distintos, dados a seguir, foram esboçados pelos alunos.
Dentre eles, o que melhor representa a função f é





Uma pessoa faz um empréstimo de R$10 600,00, com vencimento em 10 meses, a contar da
data do contrato, pagando juros simples de 18% aa.
Querendo antecipar 50% do valor do empréstimo no fim de 4 meses, mais R$2 800,00 no fim
de 8 meses, e o restante na data do vencimento, a pessoa pagará juros, no valor total de
Uma pessoa faz um empréstimo de R$10 600,00, com vencimento em 10 meses, a contar da data do contrato, pagando juros simples de 18% aa.
Querendo antecipar 50% do valor do empréstimo no fim de 4 meses, mais R$2 800,00 no fim de 8 meses, e o restante na data do vencimento, a pessoa pagará juros, no valor total de
Uma pessoa começou a fazer caminhada em torno de uma praça circular, andando sempre
no mesmo sentido, de modo que, a cada dia, a caminhada era iniciada em um ponto diferente
da praça: P1, no primeiro dia, P2, no segundo dia, P3, no terceiro dia, e assim sucessivamente.
Sabendo-se que P1, P2, P3... são pontos da circunferência que contorna a praça, tais que cada
setor  mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
Uma pessoa começou a fazer caminhada em torno de uma praça circular, andando sempre
no mesmo sentido, de modo que, a cada dia, a caminhada era iniciada em um ponto diferente
da praça: P1, no primeiro dia, P2, no segundo dia, P3, no terceiro dia, e assim sucessivamente.
Sabendo-se que P1, P2, P3... são pontos da circunferência que contorna a praça, tais que cada
setor  mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
mede 48°
, pode-se afirmar que essa pessoa iniciou a caminhada em
P1 pela segunda vez, no
O lucro obtido por um comerciante na venda de determinado produto é dado, em reais, pela função L(x) = -1/10 x2 +15x , sendo x o número de unidades vendidas e 0<x<150.
Se L(m) é o lucro máximo que o comerciante tem condições de obter, pode-se afirmar que log(L(m)/3m) é igual a
Em uma maratona de conhecimentos, o vencedor da prova sobre expressões algébricas
encontrou corretamente o resto da divisão do polinômio x10 + x9 + x8 +... + x - 9 por x2 − 1.
Esse resto é
Em uma maratona de conhecimentos, o vencedor da prova sobre expressões algébricas encontrou corretamente o resto da divisão do polinômio x10 + x9 + x8 +... + x - 9 por x2 − 1.
Esse resto é
O conjunto-imagem da função real f, tal que f(2x − 4) = 3(x − 2) + k, k constante, e f −1
(6) = 4, é
o intervalo
Uma instituição de ensino selecionou um grupo de 10 estudantes aos quais serão concedidas
bolsas de estudos para cursos de inglês ou espanhol.
Sabe-se que existem disponíveis 6 bolsas para o curso de inglês e 4 bolsas para o curso de
espanhol.
Então, o número máximo de formas distintas de distribuí-las, de modo que cada estudante receba
uma única bolsa, e X, Y e Z, participantes do grupo, recebam bolsas para o curso de Inglês
é igual a
Uma instituição de ensino selecionou um grupo de 10 estudantes aos quais serão concedidas bolsas de estudos para cursos de inglês ou espanhol.
Sabe-se que existem disponíveis 6 bolsas para o curso de inglês e 4 bolsas para o curso de espanhol.
Então, o número máximo de formas distintas de distribuí-las, de modo que cada estudante receba uma única bolsa, e X, Y e Z, participantes do grupo, recebam bolsas para o curso de Inglês é igual a

Um painel decorativo é pintado como um tabuleiro com 9 casas, sendo 4 brancas e 5 pretas,
de acordo com a figura.
Afixando-se, nesse painel, três fotos, de forma aleatória, cada uma delas dentro de uma casa
distinta, a probabilidade de essas fotos ocuparem três casas de mesma cor é,
aproximadamente, igual a

Um painel decorativo é pintado como um tabuleiro com 9 casas, sendo 4 brancas e 5 pretas, de acordo com a figura.
Afixando-se, nesse painel, três fotos, de forma aleatória, cada uma delas dentro de uma casa
distinta, a probabilidade de essas fotos ocuparem três casas de mesma cor é,
aproximadamente, igual a
Um terreno na forma de um paralelogramo tem o seu contorno desenhado, em um sistema
de coordenadas cartesianas, de modo que os pontos O, A, B e C, nessa ordem, representam
seus vértices consecutivos.
Sabendo-se que O é a origem do plano complexo, A é o afixo de z = 2(√3 +1) e B é o afixo de w = 2√3(1 + i), pode-se concluir que o ponto que representa o vértice C é o afixo de
Um terreno na forma de um paralelogramo tem o seu contorno desenhado, em um sistema de coordenadas cartesianas, de modo que os pontos O, A, B e C, nessa ordem, representam seus vértices consecutivos.
Sabendo-se que O é a origem do plano complexo, A é o afixo de z = 2(√3 +1) e B é o afixo de w = 2√3(1 + i), pode-se concluir que o ponto que representa o vértice C é o afixo de
Com o objetivo de arrecadar fundos para uma instituição beneficente, foi organizada uma
exposição de obras de arte por um determinado período, cobrando-se de cada visitante um certo
valor de entrada. No primeiro dia, foram arrecadados R$1 900,00 e, até o sexto dia de exposição,
os valores diários arrecadados cresceram segundo uma P.A. de razão r = 100. A partir do sexto
dia, esses valores decresceram segundo uma P.G. de razão q=1/2.
Sabendo-se que o valor total arrecadado excedeu a R$15 000,00, pode-se afirmar que a
exposição durou, pelo menos,
Com o objetivo de arrecadar fundos para uma instituição beneficente, foi organizada uma exposição de obras de arte por um determinado período, cobrando-se de cada visitante um certo valor de entrada. No primeiro dia, foram arrecadados R$1 900,00 e, até o sexto dia de exposição, os valores diários arrecadados cresceram segundo uma P.A. de razão r = 100. A partir do sexto dia, esses valores decresceram segundo uma P.G. de razão q=1/2.
Sabendo-se que o valor total arrecadado excedeu a R$15 000,00, pode-se afirmar que a exposição durou, pelo menos,