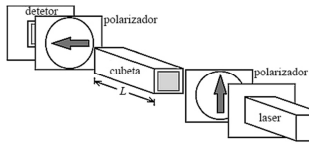
O álcool é um dos produtos de extrema importância para a
independência energética brasileira, por isso, existe a necessidade
de se desenvolver técnicas baratas que permitam avaliar alguma
propriedade dos produtos de maneira eficiente junto ao produtor.
Uma dessas técnicas é a polarimetria, que permite determinar a
concentração de sacarose em uma amostra advinda da cana-deaçúcar. A figura a seguir esquematiza o funcionamento dessa
técnica: a luz de uma fonte luminosa, normalmente um laser de
certo comprimento de onda, atravessa dois polarizadores
cruzados, estabelecendo um valor mínimo para a detecção da
intensidade da luz; entre esses polarizadores, coloca-se uma
amostra líquida de sacarose em uma cubeta; depois do segundo
polarizador (analisador), encontra-se um detector de intensidade
luminosa. A sacarose tem a propriedade de girar o plano da
polarização e é dextrógira. O grau de rotação da polarização
depende do comprimento L da cubeta, da constante de rotação ⍺ e da concentração γ da amostra, o que pode ser resumido pela
expressão ⦵ = α × L × γ, em que ⦵ é dado em graus, γ, em g/mL e
L, em dm.
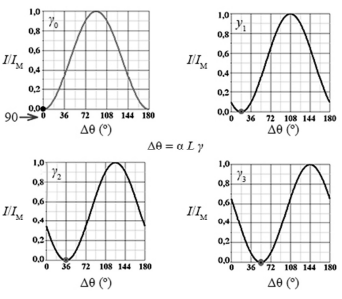
A seguir, os gráficos mostram o resultado experimental da
medida da rotação da polarização para uma amostra de sacarose
com três concentrações diferentes: γ1, γ2 e γ3. Nesses gráficos, I
representa a intensidade da luz emergente do polarímetro e IM,
um fator de normalização. O gráfico γ0 é a situação original, na
qual não há sacarose e os polarizadores estão cruzados, ou seja,
em ângulo de 90° entre si. Para essa situação específica, L = 1 dm
e a constante de rotação da sacarose é α = 58 mL∙g−1∙dm−1.