Questões UFGD sobre Matemática | Pratique com o Prisma

cabdeb39-b1

UFGD 2011 - Matemática - Progressão Aritmética - PA, Progressões

Em fevereiro de 2011, na fictícia cidade de Eutoatoatá, as temperaturas médias de cada dia do mês formaram uma progressão aritmética, com razão não nula. A temperatura do dia 27 foi igual, em módulo, à do primeiro dia do mês. A temperatura média do mês de fevereiro foi de 1°C, logo, pode-se afirmar que no décimo dia a temperatura foi de

A

12ºC negativos.

B

12ºC.

C

10ºC negativos.

D

10ºC.

E

8ºC negativos.

cac1d3e7-b1

UFGD 2011 - Matemática - Aritmética e Problemas, Porcentagem

A radioatividade de um objeto cai pela metade após 100 anos e deixa de oferecer risco de contaminação quando ela cai para menos de 5% do valor inicial. Se esse objeto estiver com 80% da sua radioatividade inicial, então,

A

será necessário esperar mais de 400 anos para que o objeto deixe de oferecer risco.

B

já se passou 50 anos do início do processo radioativo.

C

após exatamente 400 anos, este objeto ainda oferece risco.

D

não será necessário esperar 400 anos para que o objeto deixe de oferecer risco.

E

a radioatividade do objeto se extinguirá completamente após 1000 anos.

caa978ba-b1

UFGD 2011 - Matemática - Aritmética e Problemas, Porcentagem

O álcool hidratado carburante tem 96% de puro álcool e 4% de água; já o álcool anidro, que é usado como aditivo na gasolina a 22%, tem 99,5% de puro álcool e 0,5% de água. Sabendo que Pinduco abasteceu o carro com gasolina e álcool na proporção de 2:3, conclui-se que o percentual de água na mistura é de exatamente

A

2,400%

B

2,444%

C

2,440%

D

3,400%

E

3,440%

caae25da-b1

UFGD 2011 - Matemática - Aritmética e Problemas, Médias

O prefeito da cidade de Guará-Michí solicitou ao secretário de educação a idade média dos alunos da rede municipal. Os diretores não enviaram os dados dos alunos, mas a média de cada uma das escolas. A média de idade dos alunos da escola A é de 12 anos, os da escola B é de 15 anos e da escola C é de 14 anos. A escola A tem o dobro de alunos da escola B e a escola C, o triplo da escola B, logo, a média de idade dos alunos da rede municipal é

A

13,50

B

13,66

C

14,00

D

13,00

E

14,10

cab186cc-b1

UFGD 2011 - Matemática - Polígonos, Geometria Plana

Considerando o pentágono ABCDE da figura a seguir, e sabendo-se que os ângulos = 1400 e = 1200, então, a soma dos ângulos , e é

A

380°

B

280°

C

295°

D

430°

E

480°

cab5434e-b1

UFGD 2011 - Matemática - Funções, Função de 2º Grau

Seja f a função, cujo gráfico é dado a seguir.

Sabendo que f é polinomial de grau 3, então, o valor da função no ponto x=3 é igual a

A

3

B

5

C

9

D

10

E

27

cab97d29-b1

UFGD 2011 - Matemática - Probabilidade

Foi entrevistado um grupo de 55 jovens em relação a prática de esportes, sendo 17 garotos e 38 garotas. Constatou-se que cada jovem praticava somente um esporte entre vôlei e peteca, da seguinte for

Garotos Garotas
Vôlei 10 15
Peteca 7 23

Escolhido, ao acaso, uma pessoa desse grupo, pode-se afirmar que a probabilidade de essa pessoa

A

ser um garoto é de 7/17.

B

ser um garoto é de 50%, visto que o problema trata-se apenas de garotos e garotas.

C

ser um garoto e jogar peteca é 7/17.

D

jogar peteca é de 6/11.

E

jogar peteca é de 11/6.

ca987319-b1

UFGD 2011 - Matemática - Álgebra, Problemas

A diferença de idades de dois irmãos hoje é de 2 anos. Sabendo que há um ano, a idade do pai era exatamente o dobro das somas das idades dos filhos e, após 15 anos, a idade do pai será a soma das idades dos irmãos, então, a soma das três idades é

A

66

B

62

C

52

D

51

E

41

ca93e5c4-b1

UFGD 2011 - Matemática - Números Complexos

Uma trinômio do segundo grau p(x) = x² + bx + c tem como raiz o número complexo 2 - 5i . Então, o valor de (b + c) é

A

51

B

33

C

25

D

22

E

11

ca9c3c2c-b1

UFGD 2011 - Matemática - Matrizes, Álgebra Linear

Um computador atribui um número inteiro diferente a cada caractere do teclado. Para transmitir uma mensagem pela internet, esta é transformada em uma sequência de números inteiros consecutivos que é codificada do seguinte modo: A cada grupo de 4 caracteres consecutivos a, b, c, d, o computador multiplica a matriz à direita pela matriz e transmite o resultado na sequência x, y, v, w. Por exemplo, a sequência 1, 8, 11, 3 é transmitida como a sequência 10, 19, 25, 39. Então,

A

O receptor da sequência 10, 19, 25, 39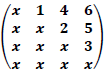 não pode decodificar exatamente qual foi a sequência original enviada.

B

O receptor só pode identificar sequências de caracteres de 4 números inteiros desde que sejam menores que 64.

C

Se o receptor recebe a sequência 8, 15, 29, 36, então, a soma dos 4 números transmitidos é 17, mas não se sabe quais são estes números.

D

Se o receptor recebe a sequência 8, 15, 29, 36, então, a soma dos 4 números transmitidos é 25, e pode-se saber exatamente quais são estes números.

E

Quaisquer sequência de 4 números, dentro das capacidades computacionais dos equipamentos, poderá ser decodificada sem ambiguidades.

ca9fd787-b1

UFGD 2011 - Matemática - Álgebra, Áreas e Perímetros, Problemas, Geometria Plana

Uma piscina de ladrilhos quadrados tem 6 ladrilhos de profundidade, 16 ladrilhos de largura e 30 ladrilhos de comprimento. Um conjunto de 16 ladrilhos justapostos tem área igual a 1 m² . Cada 1000 litros de água custa R$ 2,36, então, o custo para encher a piscina será de

A

R$ 206,80

B

R$ 106,80

C

R$ 106,20

D

R$ 104,20

E

R$ 108,80

caa5a413-b1

UFGD 2011 - Matemática - Matrizes, Álgebra Linear

Dada a matriz A(x) = considere p(x) = detA(x) em que “det” denota o determinante. Então o polinômio p(x) pode ser fatorado como

A

x(x - 1)(x - 2)(x - 3)

B

x(x - 2)(x - 2)(x - 3)

C

x(x - 3)(x - 4)(x - 5)

D

x(x - 4)(x - 5)(x - 6)

E

x(x - 1)(x - 3)(x - 4)

ca8f20c3-b1

UFGD 2011 - Matemática - Números Complexos

Um número complexo z = a + lb está (a,b) representado geometricamente por um ponto cuja distância da origem O é de uma unidade, e o segmento OP faz um ângulo de 15º com o eixo dos x (abcissas). Então, o número complexo z4 é representado por um ponto Q = (x,y), tal que

A

x = √6 + √2/4

B

y = √6 + √2/4

C

x = √3/2

D

y = √3/2

E

x = √2/2

8b9f41c9-b0

UFGD 2016 - Matemática - Aritmética e Problemas, MMC e MDC

De quatro em quatro dias Caio tem um dia de folga e de seis em seis dias Davi tem um dia de folga. Se hoje ambos folgaram, daqui quantos dias ambos folgarão novamente?

A

Seis

B

Dezoito

C

Oito

D

Vinte e quatro

E

Doze

8b7ff6b2-b0

UFGD 2016 - Matemática - Aritmética e Problemas, Razão, Proporção e Números Proporcionais

Um fabricante de doces produzirá chocolates em dois formatos, cônicos retos e cilíndricos retos, de modo que, ambas as formas apresentem mesmo volume e bases circulares com mesma área. Qual a razão entre a altura h do chocolate cônico e a altura H do chocolate cilíndrico?

A

h/H = 2

B

h/H = 3

C

h/H = 1/2

D

h/H = 1/3

E

h/H = 1

8b8449f7-b0

UFGD 2016 - Matemática - Aritmética e Problemas, Porcentagem

Na eleição para representante discente de um dos cursos da UFGD, o candidato mais votado teve 250% do número de votos do candidato menos votado. Além disso, a diferença entre o número de votos do candidato mais votado e o número de votos do candidato menos votado foi de 39. Quantos votos o candidato mais votado teve?

A

46

B

57

C

65

D

71

E

83

8b87aa89-b0

UFGD 2016 - Matemática - Aritmética e Problemas, Regra de Três

Um vídeo cujo tempo original de gravação é de sessenta minutos leva quanto tempo de reprodução ao ser assistido em velocidade de 1,25 vezes a velocidade original?

A

1 hora e 25 minutos

B

1 hora e 15 minutos

C

48 minutos

D

45 minutos

E

40 minutos

8b8d1e8d-b0

UFGD 2016 - Matemática - Seno, Cosseno e Tangente, Trigonometria, Geometria Plana, Triângulos

Considere um triângulo cujos lados medem 3a, 4a e 5a, de modo que a seja um número positivo qualquer. Determine o cosseno do menor ângulo interno deste triângulo.

A

0,8

B

0,7

C

0,6

D

0,4

E

0,2

8b94638c-b0

UFGD 2016 - Matemática - Álgebra, Problemas

Uma pensão comporta até 50 moradores e cobra mensalmente de cada morador R$200,00 mais R$5,00 por vaga desocupada. Qual a quantidade de moradores que fornece maior arrecadação à pensão?

A

50

B

45

C

35

D

20

E

15

8b7a9e4d-b0

UFGD 2016 - Matemática - Estatística

Minha nota final na disciplina de Matemática foi 6,25. Se tirei na primeira, segunda e quarta provas, respectivamente notas 6,5, 5,0 e 7,0, quanto tirei na terceira prova, se a nota final é dada pela média aritmética das notas das quatro provas?

A

5,0

B

5,5

C

6,0

D

6,5

E

7,0

Questõesde UFGD sobre Matemática