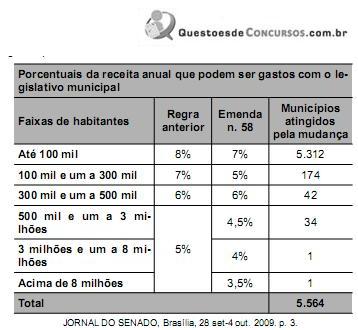
96862c97-58
UFG 2010 - Matemática - Aritmética e Problemas, Esfera, Regra de Três, Geometria Espacial
Uma confeiteira produziu 30 trufas de formato esférico com 4 cm de diâmetro cada. Para finalizar, cada unidade será coberta com uma camada uniforme de chocolate derretido, passando a ter um volume de 16π cm³. Considerando-se que, com 100 g de chocolate, obtém-se 80 mL de chocolate derretido, que quantidade de chocolate, em gramas, será necessária para cobrir as 30 trufas?
Dado: π = 3,14.
Uma confeiteira produziu 30 trufas de formato esférico com 4 cm de diâmetro cada. Para finalizar, cada unidade será coberta com uma camada uniforme de chocolate derretido, passando a ter um volume de 16π cm³. Considerando-se que, com 100 g de chocolate, obtém-se 80 mL de chocolate derretido, que quantidade de chocolate, em gramas, será necessária para cobrir as 30 trufas?
Dado: π = 3,14.
Dado: π = 3,14.
A
608
B
618
C
628
D
638
E
648