Física
Colho esta luz solar à minha volta,
No meu prisma a disperso e recomponho:
Rumor de sete cores, silêncio branco.
JOSÉ SARAMAGO
Na imagem a seguir, o triângulo ABC representa uma seção plana paralela à base de um prisma
reto. As retas n e n’ são perpendiculares aos lados AC e AB , respectivamente, e BÂC = 80°.

A medida do ângulo θ entre n e n’ é:
Física
Colho esta luz solar à minha volta,
No meu prisma a disperso e recomponho:
Rumor de sete cores, silêncio branco.
JOSÉ SARAMAGO
Na imagem a seguir, o triângulo ABC representa uma seção plana paralela à base de um prisma reto. As retas n e n’ são perpendiculares aos lados AC e AB , respectivamente, e BÂC = 80°.

A medida do ângulo θ entre n e n’ é:













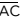 . Desse modo, a área
do triângulo ABH é igual à metade da área de ABC.
. Desse modo, a área
do triângulo ABH é igual à metade da área de ABC. 