Questõesde UERJ sobre Matemática

InícioTodas as questões
1
1
Foram encontradas 219 questões
bb025961-ba
UERJ 2017, UERJ 2017, UERJ 2017 - Matemática - Análise de Tabelas e Gráficos

No mapa mensal de um hospital, foi registrado o total de 800 cirurgias ortopédicas, sendo 440 em homens, conforme os gráficos abaixo.

De acordo com esses dados, o número total de cirurgias de fêmur realizadas em mulheres foi:

A
144
B
162
C
184
D
190
ba908856-ba
UERJ 2017, UERJ 2017 - Matemática - Análise de Tabelas e Gráficos

Segundo os paleontólogos, Lucy tinha 1,10 m de altura e 30 kg de massa corporal, sendo possível calcular seu Índice de Massa Corporal (IMC). Considere a classificação a seguir:

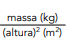Sabendo que IMC = e com base na tabela, a classificação de Lucy é:

A
pré-obesidade
B
magreza grave
C
peso adequado
D
obesidade mórbida
f07023c7-b9
UERJ 2016, UERJ 2016 - Matemática - Pirâmides, Geometria Espacial

Uma pirâmide com exatamente seis arestas congruentes é denominada tetraedro regular. Admita que a aresta do tetraedro regular ilustrado a seguir, de vértices ABCD, mede 6 cm e que o ponto médio da aresta BC é M.
O cosseno do ângulo equivale a:

A
1/2
B
1/3
C
2/3
D
2/5
e90693c5-b9
UERJ 2013, UERJ 2013 - Matemática - Pontos e Retas, Relações Métricas no Triângulo Retângulo, Geometria Analítica, Geometria Plana

O gráfico abaixo mostra o segmento de reta AB, sobre o qual um ponto C (p, q) se desloca de A até B (3, 0).

O produto das distâncias do ponto C aos eixos coordenados é variável e tem valor máximo igual a 4,5.

O comprimento do segmento AB corresponde a:

A
5
B
6
C
3√5
D
6√2
e8fe7daf-b9
UERJ 2013, UERJ 2013 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Razão, Proporção e Números Proporcionais, Geometria Plana

Na figura a seguir, estão representados o triângulo retângulo ABC e os retângulos semelhantes I, II e III, de alturas h1 , h2 e h3 respectivamente proporcionais às bases 

Se  = 4m e  = 3m, a razão 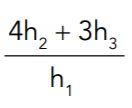 é igual a:

A
5
B
4
C
3
D
2
e8f78307-b9
UERJ 2013, UERJ 2013 - Matemática - Análise de Tabelas e Gráficos, Geometria Espacial, Poliedros

Um quadrado ABCD de centro O está situado sobre um plano α. Esse plano contém o segmento OV, perpendicular a BC, conforme ilustra a imagem:

Admita a rotação de centro O do segmento OV em um plano perpendicular ao plano a, como se observa nas imagens:


Considere as seguintes informações:
• o lado do quadrado ABCD e o segmento OV medem 1 metro;
• a rotação do segmento OV é de x radianos, sendo 0 < x ≤ π/2;
• x corresponde ao ângulo formado pelo segmento OV e o plano α;
• o volume da pirâmide ABCDV, em metros cúbicos, é igual a y.

O gráfico que melhor representa o volume y da pirâmide, em m3 , em função do ângulo x, em radianos, é:

A

B

C

D

e8fb4e9f-b9
UERJ 2013 - Matemática - Análise de Tabelas e Gráficos, Álgebra, Problemas

Admita a realização de um campeonato de futebol no qual as advertências recebidas pelos atletas são representadas apenas por cartões amarelos. Esses cartões são convertidos em multas, de acordo com os seguintes critérios:
• os dois primeiros cartões recebidos não geram multas;
• o terceiro cartão gera multa de R$ 500,00;
• os cartões seguintes geram multas cujos valores são sempre acrescidos de R$ 500,00 em relação ao valor da multa anterior.

Na tabela, indicam-se as multas relacionadas aos cinco primeiros cartões aplicados a um atleta.

Cartão amarelo recebido Valor da multa (R$)
1º -
2º -
3º 500
4º 1.000
5º 1.500

Considere um atleta que tenha recebido 13 cartões amarelos durante o campeonato.
O valor total, em reais, das multas geradas por todos esses cartões equivale a:

A
30.000
B
33.000
C
36.000
D
39.000
ed5ead41-b9
UERJ 2016 - Matemática - Álgebra Linear - Equações Lineares, Espaço Vetorial e Transformações Lineares e Matrizes, Álgebra Linear

Adaptado de portaldarmc.com.br.

No mapa, o trajeto total da tocha olímpica em território brasileiro mede cerca de 72 cm, considerando os trechos por via aérea e por terra.
A distância real, em quilômetros, percorrida pela tocha em seu trajeto completo, é de aproximadamente: 

A
3 600
B
7 000
C
36 000
D
70 000
ed0d80ce-b9
UERJ 2016 - Matemática - Seno, Cosseno e Tangente, Circunferências e Círculos, Trigonometria, Polígonos, Geometria Plana

No esquema abaixo, estão representados um quadrado ABCD e um círculo de centro P e raio r,tangente às retas AB e BC. O lado do quadrado mede 3r.
A medida θ do ângulo CÂP pode ser determinada a partir da seguinte identidade trigonométrica:

                                                               tg (α - β) =  tg(α) - tg(β)/1 + tg(α) × tg(β) 


O valor da tangente de θ é igual a:

A
0,65
B
0,60
C
0,55
D
0,50
ed04e72e-b9
UERJ 2016 - Matemática - Geometria Espacial, Cilindro

Um cilindro circular reto possui diâmetro AB de 4 cm e altura AA’ de 10 cm. O plano α, perpendicular à seção meridiana ABB’A’, que passa pelos pontos B e A’ das bases, divide o cilindro em duas partes, conforme ilustra a imagem.

O volume da parte do cilindro compreendida entre o plano α e a base inferior, em cm3 , é igual a:

A
8π
B
12π
C
16π
D
20π
ed013667-b9
UERJ 2016 - Matemática - Análise de Tabelas e Gráficos

Para combater a subnutrição infantil, foi desenvolvida uma mistura alimentícia composta por três tipos de suplementos alimentares: I, II e III. Esses suplementos, por sua vez, contêm diferentes concentrações de três nutrientes: A, B e C. Observe as tabelas a seguir, que indicam a concentração de nutrientes nos suplementos e a porcentagem de suplementos na mistura, respectivamente. 

                        Concentração dos Suplementos Alimentares (g/kg)
Nutriente                                             I             II             III
        A                                                 0,2         0,5             0,4
        B                                                 0,3         0,4             0,1
        C                                                 0,1         0,4             0,5


Suplemento Alimentar         Quantidade na Mistura (%)
                    I                                             45
                    II                                            25
                    III                                           30

A quantidade do nutriente C, em g/kg, encontrada na mistura alimentícia é igual a:

A
0,235
B
0,265
C
0,275
D
0,295
ecfa9e12-b9
UERJ 2016 - Matemática - Aritmética e Problemas, Porcentagem

Um comerciante, para aumentar as vendas de seu estabelecimento, fez a seguinte promoção para determinado produto:

COMPRE 4 UNIDADES E LEVE 5

Essa promoção representa um desconto de x% na venda de 5 unidades.
O valor de x é igual a:

A
10
B
15
C
20
D
25
660affd3-b9
UERJ 2015, UERJ 2015 - Matemática - Áreas e Perímetros, Geometria Plana

Na figura abaixo, estão representados dois círculos congruentes, de centros C1 e C2 , pertencentes ao mesmo plano α. O segmento mede 6 cm.


A área da região limitada pelos círculos, em cm2 , possui valor aproximado de:

A
108
B
162
C
182
D
216
65f9b449-b9
UERJ 2015, UERJ 2015 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Álgebra, Equação do 2º Grau e Problemas do 2º Grau, Produtos Notáveis e Fatoração

Um fabricante produz embalagens de volume igual a 8 litros no formato de um prisma reto com base quadrada de aresta a e altura h. Visando à redução de custos, a área superficial da embalagem é a menor possível. Nesse caso, o valor de a corresponde, em decímetros, à raiz real da seguinte equação:

4a - 32/a² = 0

As medidas da embalagem, em decímetros, são:

A
a = 1 ; h = 2
B
a = 1 ; h = 4
C
a = 2 ; h = 4
D
a = 2 ; h = 2