Questõesde UDESC sobre Matemática
O número de termos da P.G. ( a, b, 10/27, c, 2/9,... 2/25, d, e) é igual a:
A expressão 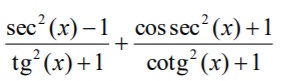 é igual a:
é igual a:
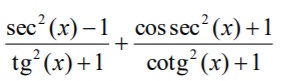 é igual a:
é igual a:Sejam A e B duas matrizes tais que A = 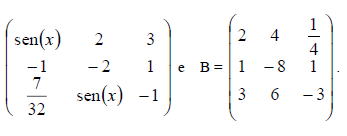
O conjunto solução para que o determinante da matriz A . B seja igual a zero é:
Sejam A e B duas matrizes tais que A = 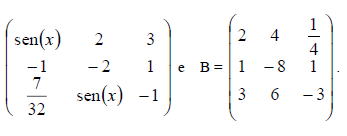
O conjunto solução para que o determinante da matriz A . B seja igual a zero é:
As instruções da Figura 4 referem-se ao início da construção de um avião de origami (papel dobrado).

Figura 4:
Passos para construir um avião
Se a folha de papel inicial tem 25cm x 40cm, o lado maior do triângulo isósceles CEF, formado após a última
dobra indicada, é
As instruções da Figura 4 referem-se ao início da construção de um avião de origami (papel dobrado).

Figura 4:
Passos para construir um avião Se a folha de papel inicial tem 25cm x 40cm, o lado maior do triângulo isósceles CEF, formado após a última dobra indicada, é


No sistema de coordenadas cartesianas um ponto é localizado com base em duas coordenadas, x e y, obtidas,respectivamente, pela distância a dois eixos ordenados.
Um outro sistema de coordenadas bastante utilizado é o polar, em que um ponto é determinado também por meio de duas coordenas r e θ, sendo r a distância de um ponto a outro, denominado de origem e θ o ângulo formado no sentido anti-horário com o eixo polar, o qual é uma reta passando pela origem. Na Figura 3 tem-se a representação do ponto P( 2, π/3) em coordenadas polares.

O gráfico que melhor representa o conjunto de pontos (
r , θ ), em coordenadas polares, sendo
r = θ , é uma:

Seja r uma reta passando por um ponto A e seja P um ponto não pertencente à reta, de tal forma que a distância
entre os pontos P e A seja de 4 unidades de comprimento e o ângulo formado entre a reta r e o segmento AP
seja de 30 graus, conforme a Figura 2.

Sabendo-se que a equação da reta r é y = 3 e que a reta que passa pelos pontos A e P corta o eixo y no ponto
(0,2), então a soma dos quadrados das coordenadas do ponto P é igual a:

Uma loja de material para pintura fabrica tintas de cores personalizadas, usando uma máquina que mistura até
3 cores iniciais em proporções que podem ser ajustadas de 20% em 20%. Sabendo que há 4 cores iniciais para
se escolher, o número de cores que podem ser oferecidas, incluindo as iniciais puras, é:
Um engenheiro precisa projetar uma rampa de acesso com inclinação constante. A altura da porta de entrada em relação à rua é de 150 cm e o espaço para construção da rampa é de 215 cm. Sendo α o ângulo de inclinação dessa rampa, é correto afirmar que:
Os gráficos das funçõesf (x) = 1 -x, g(x) = 6x e h(x) = -x2 + 2x + 5 estão ilustrados na Figura 1.

Analise as sentenças abaixo, em relação às informações anteriores.
I. f(x) ≤ h(x) ≤ g(x) se, e somente se, 1 ≤ x ≤ 4
II. f(x) ≤ h(x) ≤ g(x) se, e somente se, 0 ≤ x ≤ 4
III; h(x) ≤ g(x) ≤ f (x) se, e somente se, -2 ≤ x ≤ -1
IV. g(x) ≤ f(x) ≤ h(x) se, e somente se, -2 ≤ x ≤ 0
V. g(x) ≤ h(x) ≤ f(x) se, e somente se, -2 ≤ x ≤ -1
Assinale a alternativa que contém o número de sentença(s) verdadeira(s).
Os gráficos das funçõesf (x) = 1 -x, g(x) = 6x e h(x) = -x2 + 2x + 5 estão ilustrados na Figura 1.

Analise as sentenças abaixo, em relação às informações anteriores.
I. f(x) ≤ h(x) ≤ g(x) se, e somente se, 1 ≤ x ≤ 4
II. f(x) ≤ h(x) ≤ g(x) se, e somente se, 0 ≤ x ≤ 4
III; h(x) ≤ g(x) ≤ f (x) se, e somente se, -2 ≤ x ≤ -1
IV. g(x) ≤ f(x) ≤ h(x) se, e somente se, -2 ≤ x ≤ 0
V. g(x) ≤ h(x) ≤ f(x) se, e somente se, -2 ≤ x ≤ -1
Assinale a alternativa que contém o número de sentença(s) verdadeira(s).
Ana tem uma impressora 3D que utiliza o polímero PLA (poliácido láctico) para imprimir objetos. Ela comprou
1 quilograma de PLA em formato de fio cilíndrico com diâmetro de 1,75 milímetro, no valor de R$120,00. Para
imprimir um objeto A, o programa de impressão estima gastar 12 metros do material. Sabendo que cada metro
de PLA tem 3 gramas, o valor gasto em filamento para imprimir esse objeto é:
Uma pirâmide regular de base hexagonal tem o vértice sobre uma semiesfera e a base inscrita na base desta
semiesfera. Sabendo que a aresta lateral dessa pirâmide mede 10 cm, então o volume é igual a:
Sejam (16,18, 20, ...) e (1/2, 3, 11/2, ...) duas progressões aritméticas. Estas duas progressões
apresentarão somas iguais, para uma mesma quantidade de termos somados, quando o valor
da soma for igual a:


A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g
e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma
nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada
item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:
A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:


Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 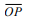 mede
5cm.
mede
5cm.

Sabendo que o segmento 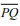 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 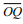 mede:
mede:
Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 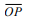 mede
5cm.
mede
5cm.

Sabendo que o segmento 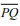 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 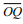 mede:
mede:


Em um triângulo retângulo ABC são construídos três triângulos equiláteros, conforme Figura 1.

Com base na informação e na Figura 1, analise as proposições.
I – A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II – Se a área do triângulo ABC é 6 cm2 e a altura do triângulo CBF é √30cm, então o perímetro
do triângulo ABC é
2 . (4 + √10) cm.
III – Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos
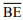 e
e 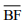 é igual ao comprimento do segmento
é igual ao comprimento do segmento 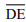 .
.
Assinale a alternativa correta.
Em um triângulo retângulo ABC são construídos três triângulos equiláteros, conforme Figura 1.

Com base na informação e na Figura 1, analise as proposições.
I – A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II – Se a área do triângulo ABC é 6 cm2 e a altura do triângulo CBF é √30cm, então o perímetro do triângulo ABC é 2 . (4 + √10) cm.
III – Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos
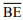 e
e 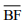 é igual ao comprimento do segmento
é igual ao comprimento do segmento 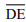 .
.
Assinale a alternativa correta.


A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos
babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz
quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números
procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e
Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:
A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:


Em 1958, como trote para os calouros da universidade de Harvard, nos Estados Unidos, um
grupo de estudantes precisou medir o comprimento da ponte de Harvard (entre Boston e
Cambridge, em Massachusetts), usando como padrão de medida um dos próprios estudantes,
um rapaz chamado Oliver R. Smoot. Após horas de medição, com o estudante deitando-se no
chão e levantando-se sucessivas vezes para as medidas, concluiu-se que a ponte tinha 364,4
smoots, +/- 1 orelha.
A brincadeira fez tanto sucesso e a medição tornou-se tão popular que, na década de 1980, a
ponte foi reformada pela prefeitura, que encomendou blocos de concreto personalizados de 1
smoot de comprimento para a reforma, eternizando as marcações colocadas no solo, que hoje
já constam até no sistema de conversão de medidas da ferramenta Google.
Ainda mais interessante é o fato de que, alguns anos após formado, Oliver Smoot tornou-se
diretor da ANSI, o Instituto Nacional Americano de Padrões (“American National Standards
Institute”) e depois presidente da ISO, a Organização Internacional para Padronização
(“International Organization for Standardization”).
Sabendo que Oliver Smoot tinha 5 pés e 7 polegadas de altura na ocasião da medida,
desprezando o erro de +/- 1 orelha, e assumindo 1 pé = 30,5 cm e 1 polegada = 2,5 cm, o
comprimento da ponte é:


Analise as proposições abaixo.
I – O produto de uma matriz linha por uma matriz linha é uma matriz linha.
II – Uma matriz identidade elevada ao quadrado é uma matriz identidade.
III - O produto de uma matriz por sua transposta é a matriz identidade.
Assinale a alternativa correta.
Analise as proposições abaixo.
I – O produto de uma matriz linha por uma matriz linha é uma matriz linha.
II – Uma matriz identidade elevada ao quadrado é uma matriz identidade.
III - O produto de uma matriz por sua transposta é a matriz identidade.
Assinale a alternativa correta.


Uma coroa cilíndrica é a região espacial situada entre dois cilindros concêntricos de mesma
altura, um com raio
R
e outro com raio
r
, sendo
r < R
. Se a altura, o volume e a soma das
medidas dos raios dessa coroa cilíndrica são, respectivamente,
4
cm,
4,25π cm3 e
4,25
cm,
então a área total de sua superfície é:

