Sejam A e B duas matrizes tais que A = 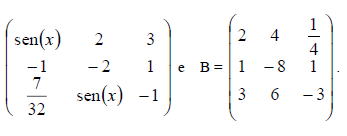
O conjunto solução para que o determinante da matriz A . B seja igual a zero é:
Sejam A e B duas matrizes tais que A = 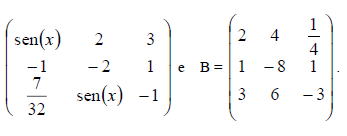
O conjunto solução para que o determinante da matriz A . B seja igual a zero é:
Sejam A e B duas matrizes tais que A = 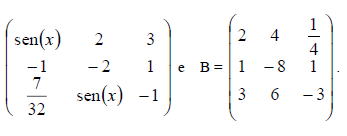
O conjunto solução para que o determinante da matriz A . B seja igual a zero é:
As instruções da Figura 4 referem-se ao início da construção de um avião de origami (papel dobrado).

Figura 4:
Passos para construir um avião Se a folha de papel inicial tem 25cm x 40cm, o lado maior do triângulo isósceles CEF, formado após a última dobra indicada, é




Os gráficos das funçõesf (x) = 1 -x, g(x) = 6x e h(x) = -x2 + 2x + 5 estão ilustrados na Figura 1.

Analise as sentenças abaixo, em relação às informações anteriores.
I. f(x) ≤ h(x) ≤ g(x) se, e somente se, 1 ≤ x ≤ 4
II. f(x) ≤ h(x) ≤ g(x) se, e somente se, 0 ≤ x ≤ 4
III; h(x) ≤ g(x) ≤ f (x) se, e somente se, -2 ≤ x ≤ -1
IV. g(x) ≤ f(x) ≤ h(x) se, e somente se, -2 ≤ x ≤ 0
V. g(x) ≤ h(x) ≤ f(x) se, e somente se, -2 ≤ x ≤ -1
Assinale a alternativa que contém o número de sentença(s) verdadeira(s).
Na Figura 2 sem escala, o raio da circunferência de centro
O
é
r = 3cm
e o segmento 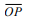 mede
5cm.
mede
5cm.

Sabendo que o segmento 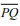 tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento
tangencia a circunferência no ponto
T,
pode-se dizer que o
segmento 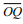 mede:
mede:




A Tabela 1 representa a tabela nutricional de um determinado tablete de chocolate de 100 g.
Tabela 1 – Informação Nutricional: Porção 1/4 do tablete

A empresa que produz este chocolate pretende reduzir o tamanho do tablete de 100g para 85g e, para isto, precisará atualizar os valores da Tabela nutricional. Além disso, será incluída uma nova coluna, que conterá os valores diários percentuais de ingestão (VD%) referentes a cada item, com base em uma dieta de 2000 Kcal, de acordo com a Tabela 2.
Tabela 2 - Valores diários de referência de nutrientes

Após a atualização da Tabela 1, o percentual do recomendado diário de carboidratos ingeridos
em uma porção do novo tablete será equivalente a:




Analise as proposições abaixo.
I – O produto de uma matriz linha por uma matriz linha é uma matriz linha.
II – Uma matriz identidade elevada ao quadrado é uma matriz identidade.
III - O produto de uma matriz por sua transposta é a matriz identidade.
Assinale a alternativa correta.




Em um triângulo retângulo ABC são construídos três triângulos equiláteros, conforme Figura 1.

Com base na informação e na Figura 1, analise as proposições.
I – A soma das áreas dos triângulos ACD e ABE é igual à área do triângulo CBF.
II – Se a área do triângulo ABC é 6 cm2 e a altura do triângulo CBF é √30cm, então o perímetro do triângulo ABC é 2 . (4 + √10) cm.
III – Se o triângulo ABC for isósceles, então a soma dos comprimentos dos segmentos
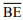 e
e 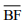 é igual ao comprimento do segmento
é igual ao comprimento do segmento 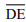 .
.
Assinale a alternativa correta.


A regra para encontrar dois números cuja soma e cujo produto são dados, era enunciada pelos babilônios como “Eleve ao quadrado a metade da soma subtraia o produto e extraia a raiz quadrada da diferença. Some ao resultado a metade da soma. Isso dará o maior dos números procurados. Subtraia-o da soma para obter o outro número.” (LIMA, Elon Lages. Números e Funções Reais. SBM, 2013. Coleção PROFMAT. p.108.)
Atualmente a fórmula que dá a resposta para esse problema é conhecida como:


O valor de
x . y com x,y 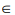 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:


A soma de todas as raízes reais da função ƒ(x) = cotg2 (x) - 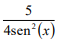 + 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:
+ 2 pertencentes ao
intervalo [π/2 , 3π] é igual a:


 . Se o
volume desse prisma triangular é 12 u.v., o valor da soma das abscissas dos vértices do
triângulo ABC é:
. Se o
volume desse prisma triangular é 12 u.v., o valor da soma das abscissas dos vértices do
triângulo ABC é: 
