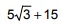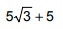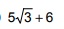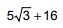Questões UFRN sobre Trigonometria | Pratique com o Prisma

119c1aae-f5

UFRN 2012 - Matemática - Seno, Cosseno e Tangente, Trigonometria, Geometria Plana, Ângulos - Lei Angular de Thales

A escadaria ao lado tem oito batentes no primeiro lance e seis, no segundo lance de escada. Sabendo que cada batente tem 20cm de altura e 30cm de comprimento (profundidade), a tangente do ângulo CÂD mede:

A

9/10

B

14/15

C

29/30

D

1

d582a61c-de

UFRN 2007, UFRN 2007 - Matemática - Trigonometria, Funções Trigonométricas e Funções Trigonométricas Inversas

A equação (Sen x)2 – 5(Sen x) + 6 = 0

A

admite mais de duas raízes.

B

admite exatamente duas raízes.

C

admite uma única raiz.

D

não admite raízes.

c498e214-4a

UFRN 2009 - Matemática - Trigonometria

Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

Nesse caso, as medidas dos segmentos correspondem, respectivamente, a

A

sen x , sec x e cot gx .

B

cos x , sen x e tgx .

C

cos x , sec x e cossec x .

D

tgx , cossec x e cos x .

3c69b1dc-4a

UFRN 2009 - Matemática - Trigonometria

Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

Nesse caso, as medidas dos segmentos correspondem, respectivamente, a

A

sen x , sec x e cot gx.

B

cos x , sen x e tgx.

C

cos x , sec x e cos sec x.

D

tgx , cos sec x e cos x.

a3949585-4a

UFRN 2009 - Matemática - Seno, Cosseno e Tangente, Trigonometria, Círculo Trigonométrico

Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

A

sen x, sec x e cot gx

B

cos x , sen x e tg x.

C

cos x, sec x e cossec x .

D

tg x, cos sec x e cos x .

3413e4a2-4b

UFRN 2008, UFRN 2008 - Matemática - Trigonometria, Geometria Plana, Triângulos

Para medir a altura de uma árvore, da qual não podia aproximar-se, um ambientalista colocou, a certa distância dessa árvore, um cavalete de 1 m de altura e observou seu ponto mais alto,
segundo um ângulo de 30° . Aproximando-se mais 10 m, observou o mesmo ponto segundo um ângulo de 45° , conforme a figura abaixo.

Com esse procedimento, o ambientalista obteve como resultado que a altura da árvore era de:

A

5 √ 3 + 15

B

5√3 +5

C

5√3 + 6

D

5√3 + 16

e754220c-4b

UFRN 2008 - Matemática - Relações Trigonométricas no Triângulo Retângulo, Leis dos Senos e Cossenos., Trigonometria, Geometria Plana

Para medir a altura de uma árvore, da qual não podia aproximar-se, um ambientalista colocou, a certa distância dessa árvore, um cavalete de 1 m de altura e observou seu ponto mais alto, segundo um ângulo de 30° . Aproximando-se mais 10 m, observou o mesmo ponto segundo um ângulo de 45° , conforme a figura abaixo.

Com esse procedimento, o ambientalista obteve como resultado que a altura da árvore era de:

A

B

C

D

Questõesde UFRN sobre Trigonometria

A escadaria ao lado tem oito batentes no primeiro lance e seis, no segundo lance de escada. Sabendo que cada batente tem 20cm de altura e 30cm de comprimento (profundidade), a tangente do ângulo CÂD mede:

A equação (Sen x)2 – 5(Sen x) + 6 = 0

Considere a figura abaixo, na qual a circunferência tem raio igual a 1. Nesse caso, as medidas dos segmentos correspondem, respectivamente, a

Considere a figura abaixo, na qual a circunferência tem raio igual a 1. Nesse caso, as medidas dos segmentos correspondem, respectivamente, a

Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

Nesse caso, as medidas dos segmentos correspondem, respectivamente, a

Considere a figura abaixo, na qual a circunferência tem raio igual a 1.

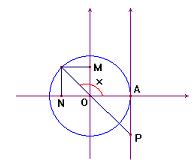
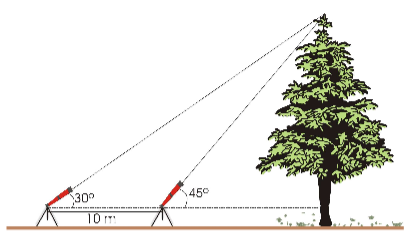
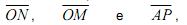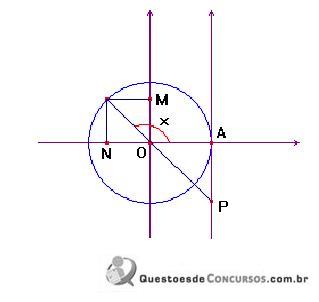
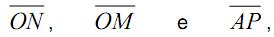Nesse caso, as medidas dos segmentos correspondem, respectivamente, a