Questõessobre Triângulos
O diâmetro de uma circunferência circunscrita a um triângulo ABC,
onde  = 75º, B = 60º e a = 6( √6 + √2 ) cm, é igual a:
Marcelo precisou subir para arrumar
um telhado, colocou uma escada de 8 metros
formando um ângulo de 300
com a horizontal, quando
Marcelo chegou no topo da escada mediu a distância
de lá até ao chão e encontrou:





Considere o ângulo segundo o qual um observador vê uma torre. Esse ângulo duplica quando ele se aproxima
160 m e quadruplica quando ele se aproxima mais 100 m, como mostra o esquema abaixo.

A altura da torre, em metros, equivale a:

Em um triângulo, as medidas de seus lados, em metros, são três números inteiros consecutivos e a medida do
maior ângulo é o dobro da medida do menor. A medida do menor lado deste triângulo é
Considere os triângulos I, II e III caracterizados abaixo através das medidas de seus lados.
- triângulo I: 9, 12 e 15. - triângulo II: 5, 12 e 13. - triângulo III: 5, 7 e 9.
Quais são os triângulos retângulos com as medidas dos lados em progressão aritmética?
O projeto de madeiramento é fundamental para a construção de um bom telhado em uma
residência.
Na figura, temos a vista frontal do madeiramento de um telhado. O triângulo ABC é isósceles
de base BC tal que
 = 120o . Observa-se também que os segmentos DE e FG são
perpendiculares à base BC.

De acordo com os dados acima, a medida do ângulo
BÊD
é
O projeto de madeiramento é fundamental para a construção de um bom telhado em uma residência.
Na figura, temos a vista frontal do madeiramento de um telhado. O triângulo ABC é isósceles de base BC tal que  = 120o . Observa-se também que os segmentos DE e FG são perpendiculares à base BC.

De acordo com os dados acima, a medida do ângulo
BÊD
é
Na figura abaixo, destacamos as medidas de BC = 10 m e SR = 2,3 m. Os valores de x e y são:

Na figura abaixo, destacamos as medidas de BC = 10 m e SR = 2,3 m. Os valores de x e y são:

Considere o triângulo isósceles ABC, tal que AB = BC = 10 cm e CA = 12 cm. A rotação desse triângulo em torno de um eixo que contém o lado AB gera um sólido cujo volume, em centímetros cúbicos, é:
Para se calcular a altura de uma torre, utilizou-se o seguinte procedimento ilustrado na figura: um aparelho (de
altura desprezível) foi colocado no solo, a uma certa distância da torre, e emitiu um raio em direção ao ponto mais
alto da torre. O ângulo determinado entre o raio e o solo foi de α = π/3 radianos. A seguir, o aparelho foi
deslocado 4 metros em direção à torre e o ângulo então obtido foi de β radianos, com tg β = 3√3.

É correto afirmar que a altura da torre, em metros, é:

O topo de uma estátua T se encontra a uma distância de 2√3 metros de um ponto P, localizado 3
no solo. Sabendo que o segmento PT forma um ângulo de 60o
com a horizontal, a altura da
estátua é dada, em metros, por:
Considere o triângulo abaixo:

Uma condição necessária para que esse triângulo exista é:
Considere o triângulo abaixo:

Uma condição necessária para que esse triângulo exista é:
Considere os triângulos I, II e III caracterizados abaixo através das medidas de seus lados.
- triângulo I: 9, 12 e 15. - triângulo II: 5, 12 e 13. - triângulo III: 5, 7 e 9.
Quais são os triângulos retângulos com as medidas dos lados em progressão aritmética?
Para sustentação de uma árvore, colocaram-se dois suportes, BD e CD tal que ABD = 45o, ACD = 30o e AB = 5 m, conforme demonstrado nesta ilustração.

A distância BC entre os suportes em metros é:
Para sustentação de uma árvore, colocaram-se dois suportes, BD e CD tal que ABD = 45o, ACD = 30o e AB = 5 m, conforme demonstrado nesta ilustração.

A distância BC entre os suportes em metros é:




A falta de oportunidade em algumas regiões de conflito faze com que uma parte da população recorra a
embarcações clandestinas para buscar uma vida
melhor nos países vizinhos.
A figura a seguir mostra uma rota de travessia entre
as cidades A e B.

Com base na figura, qual é a distância entre as
cidades A e B?

Dois postes, um de 10m e outro de 6m, devem
ser sustentados, respectivamente, por cabos de
aço de comprimentos a e b, conforme ilustra
a figura abaixo.

Os pontos de fixação F1, F2 e F3 devem ser
determinados de modo que a quantidade de
cabo de aço seja mínima.
A distância do ponto F2 até a base do poste
menor deverá ser:

A casa central de uma fazenda situa-se a 9 km,
contados ao longo de um caminho
perpendicular à estrada reta que limita a
fazenda. Na beira da estrada e a uma distância
de 15 km da casa central, o fazendeiro
construiu uma casa para seu filho. O fazendeiro
agora quer construir, na beira da mesma
estrada, um escritório que fique igualmente
distanciado da casa do filho e da casa central.

A distância comum deverá ser:

Considerando um triângulo ABC e sabendo-se que
as medidas dos ângulos A e B são, respectivamente,
30º e 45º e que a medida do lado BC é igual a 4 cm;
então, o lado AC vale

O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que 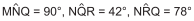 e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede

O triângulo QRN, na figura, foi obtido, girando-se o triângulo MNO em torno do ponto N.
Sabendo-se que 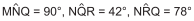 e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede
e, considerando-se P o ponto de intersecção
dos segmentos OR e QN, pode-se afirmar que o ângulo mede

Estudos mostraram a viabilidade da construção de uma ponte ligando uma cidade litorânea a
uma ilha, a partir de um ponto P ou de um ponto Q da costa, distantes 2400m um do outro,
até um ponto I da referida ilha.
Sabe-se que se a ponte for construída a partir de P ou de Q, formará com PQ ângulos de 45º
e 60º, respectivamente, e que, nas duas situações, o custo de construção é de 100 unidades
monetárias por metro linear.
Com base nessas informações e considerando-se sen 75º = 0,96, √2=1,4 e √3=1,7, pode-se
afirmar que, optando-se pela construção da ponte menor, haverá uma economia, em unidades
monetárias, de

Estudos mostraram a viabilidade da construção de uma ponte ligando uma cidade litorânea a uma ilha, a partir de um ponto P ou de um ponto Q da costa, distantes 2400m um do outro, até um ponto I da referida ilha.
Sabe-se que se a ponte for construída a partir de P ou de Q, formará com PQ ângulos de 45º e 60º, respectivamente, e que, nas duas situações, o custo de construção é de 100 unidades monetárias por metro linear.
Com base nessas informações e considerando-se sen 75º = 0,96, √2=1,4 e √3=1,7, pode-se afirmar que, optando-se pela construção da ponte menor, haverá uma economia, em unidades monetárias, de