Questõessobre Sistemas de Numeração e Operações Fundamentais

Sendo a e b números reais positivos quaisquer, considere as afirmações abaixo.

I - Se a > b então ax >bx , para qualquer x ∈ R.

II - Se a > b >1, então .

III- Se a > b , então √a > √b .

Quais estão corretas?

Leia o texto a seguir.

No Brasil, o sistema de voto proporcional funciona assim: aplicam-se os chamados quocientes eleitoral e partidário. O quociente eleitoral é definido pela soma do número de votos válidos (V) – que são os votos de legenda e os votos nominais, excluindo-se os brancos e os nulos – dividida pelo número de cadeiras em disputa (C).

A partir daí, calcula-se o quociente partidário, queéoresultado do número de votos válidos obtidos pelo partido isolado ou pela coligação, dividido pelo quociente eleitoral. O quociente partidário é um número fundamental, pois ele indica quantas cadeiras poderão ser ocupadas pelos candidatos aptos do respectivo partido ou coligação.

Adaptado de Revista Eletrônica da Escola Judiciária Eleitoral. Número 5. Ano 3.

Considere que a eleição para vereador em Amado Florêncio funciona como descrito anteriormente. Suponha que existam 12 cadeiras em disputa e que nesta eleição para vereador a soma do número dos votos válidos seja de 3996. A coligação “Por uma Nova Amado Florêncio” obteve 333 votos válidos. Já a coligação “Amado Florêncio Renovada” obteve 666 votos válidos.

Assinale a alternativa que apresenta, correta e respectivamente, o quociente partidário dessas coligações: “Por uma Nova Florêncio” e “Amado Florêncio Renovada”.

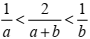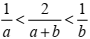Uma estratégia para obter efeito humorístico em quadrinhos é atribuir a objetos abstratos características e ações tipicamente humanas. A figura a seguir é um exemplo de aplicação desse recurso.

Supondo que cada número diga uma verdade matemática sobre si mesmo, relacione as frases (de I a IV) aos balões de diálogo (de A a D).

I. Meu cubo é irracional.

II. Sou racional.

III. Sou puramente imaginário.

IV. Meu inverso multiplicativo coincide com meu conjugado.

Assinale a alternativa que contém a associação correta.

Sejam p e q números inteiros.

A sentença verdadeira é:

1. Em um aeroporto, os passageiros devem submeter suas bagagens a uma das cinco máquinas de raio-X disponíveis ao adentrarem a sala de embarque. Num dado instante, o tempo gasto por essas máquinas para escanear a bagagem de cada passageiro e o número de pessoas presentes em cada fila estão apresentados em um painel, como mostrado na figura.

Um passageiro, ao chegar à sala de embarque desse aeroporto no instante indicado, visando esperar o menor tempo possível, deverá se dirigir à máquina

Sejam x, y e z números reais tais que -1 < x < 0, 0 < y <1 e z −2 < z <− 1.

Dos números abaixo, o que é necessariamente positivo é

Casos de febre amarela desde o início de 2017:

• confirmados → 779;

• suspeitos → 435.

Mortes entre os casos confirmados: 262.

Suponha que todos os casos suspeitos tenham sido comprovados, e que a razão entre o número de mortes e o de casos confirmados permaneça a mesma.

Nesse caso, com as novas comprovações da doença, o número total de mortos por febre amarela estaria mais próximo de:

Enquanto as lâmpadas comuns têm 8 mil horas de vida útil, as lâmpadas LED têm 50 mil horas.

MetroCuritiba, 18 ago. 2011 (adaptado).

De acordo com a informação e desprezando possíveis algarismos na parte decimal, a lâmpada LED tem uma durabilidade de

Uma loja decide premiar seus clientes. Cada cliente receberá um dos seis possíveis brindes disponíveis, conforme sua ordem de chegada na loja. Os brindes a serem distribuídos são: uma bola, um chaveiro, uma caneta, um refrigerante, um sorvete e um CD, nessa ordem. O primeiro cliente da loja recebe uma bola, o segundo recebe um chaveiro, o terceiro recebe uma caneta, o quarto recebe um refrigerante, o quinto recebe um sorvete, o sexto recebe um CD, o sétimo recebe uma bola, o oitavo recebe um chaveiro, e assim sucessivamente, segundo a ordem dos brindes.

O milésimo cliente receberá de brinde um(a)

Em uma casa, há um espaço retangular medindo 4 m por 6 m, onde se pretende colocar um piso de cerâmica resistente e de bom preço. Em uma loja especializada, há cinco possibilidades de pisos que atendem às especificações desejadas, apresentadas no quadro:

Levando-se em consideração que não há perda de material, dentre os pisos apresentados, aquele que implicará o menor custo para a colocação no referido espaço é o piso

Em um jogo educativo, o tabuleiro é uma representação da reta numérica e o jogador deve posicionar as fichas contendo números reais corretamente no tabuleiro, cujas linhas pontilhadas equivalem a 1 (uma) unidade de medida. Cada acerto vale 10 pontos.

Na sua vez de jogar, Clara recebe as seguintes fichas:

Para que Clara atinja 40 pontos nessa rodada, a figura que representa seu jogo, após a colocação das fichas no tabuleiro, é:

O cometa Halley orbita o Sol numa trajetória elíptica periódica. Ele foi observado da Terra nos anos de 1836 e 1911. Sua última aparição foi em 1986 e sua próxima aparição será em 2061.

Qual é o ano da segunda aparição do cometa anterior ao ano de 2012?