Questõessobre Seno, Cosseno e Tangente
O menor número real positivo que satisfaz a equação
2cosx - 1 = 0 é:
Sendo x igual ao cosseno de 2 radianos e y igual ao
seno de 2 radianos, conclui-se que
No círculo trigonométrico seguinte, dado um arco 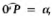 a
área do triângulo hachurado, em função da medida do arco, é
igual a
a
área do triângulo hachurado, em função da medida do arco, é
igual a

No círculo trigonométrico seguinte, dado um arco 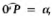 a
área do triângulo hachurado, em função da medida do arco, é
igual a
a
área do triângulo hachurado, em função da medida do arco, é
igual a



Se x e y são números reais, tais que 0 < x < π/2, 0 < y < π/2, sen(x) = 4/5 e cos(y) = 1/3, então o quociente  é igual a
é igual a
Se x e y são números reais, tais que 0 < x < π/2, 0 < y < π/2, sen(x) = 4/5 e cos(y) = 1/3, então o quociente  é igual a
é igual a


A figura a seguir exibe um pentágono em que quatro lados
consecutivos têm comprimentos a, b, c e d. Se a sequência
(a, b, c, d) é uma progressão geométrica de razão q > 1,
então tan θ é igual a


Sejam x,y ∈ (0,π/2), tais que cos(x)= 4/5 e sen(y)= 5/13. Podemos concluir que tg (x+y) é igual a:
Seja α um número real tal que a equação
2cos(x)+10 = 2α tem solução. Nessas condições,
O valor de sen  é igual a
é igual a
O valor de sen  é igual a
é igual a
Sobre trigonometria, analise as
assertivas e assinale a alternativa que
aponta as corretas.
I. cos(x) = 2 cos2 (x/2) - 1 .
II. O valor de (1 + cotg2 x) (1 - cos2 x), para x ≠ kπ, com k inteiro, é igual a 1.
III. A medida do arco trigonométrico da
1ª volta positiva, côngruo ao arco de
medida -40°, é 40°.
IV. tg 50° tg 310° < 0
tg 310° < 0
Sobre trigonometria, analise as assertivas e assinale a alternativa que aponta as corretas.
I. cos(x) = 2 cos2 (x/2) - 1 .
II. O valor de (1 + cotg2 x) (1 - cos2 x), para x ≠ kπ, com k inteiro, é igual a 1.
III. A medida do arco trigonométrico da 1ª volta positiva, côngruo ao arco de medida -40°, é 40°.
IV. tg 50° tg 310° < 0
tg 310° < 0
O valor de  é
é
O valor de  é
é
Para se trabalhar com a “escala inimaginável de tempo” mencionada no último parágrafo do texto, poderia ser feita uma transformação que associa cada número da escala a um bem menor, de modo que a quantidade de zeros fosse drasticamente reduzida. Por exemplo, o número 10100 (1 seguido de 100 zeros) pode ser associado ao número 100. A função matemática que tem essa propriedade é a


Considerando o texto acima, julgue o item e assinale a
opção correta.
Seja x um número real tal que sen x + cos x = 0,2. Logo,
| sen x − cos x| é igual a
A expressão

é equivalente a:

é equivalente a:
A figura mostra o ângulo de visão que um mesmo observador tem de uma estrutura de caixa d’água em dois pontos diferentes.
Sabe-se que a altura dos olhos, em relação ao piso plano sobre o qual a estrutura está apoiada perpendicularmente, é
exatamente a metade da altura da estrutura da caixa d’água, e que a distância entre os dois pontos de observação é de
2 metros.

A partir dessas informações, é possível determinar que a altura da estrutura da caixa d’água, em metros, é igual a

“...tudo teria começado com a haste vertical ao sol, que
projetava sua sombra num plano horizontal demarcado.”
Com um ângulo de inclinação de 30°, em relação ao solo
plano, os raios solares incidindo sobre uma haste vertical
de 2,5 m de comprimento geram uma sombra de x m. Um
pouco mais tarde, quando o ângulo de inclinação dos raios
solares é de 45° graus, a mesma sombra gerada agora é
de y m. A diferença ente x e y é de, aproximadamente,
sen 30° = 0,5 cos 30°= 0,866 tg 30° = 0,577
sen 45° = 0,707 cos 45°= 0,707 tg 45° = 1
“...tudo teria começado com a haste vertical ao sol, que projetava sua sombra num plano horizontal demarcado.” Com um ângulo de inclinação de 30°, em relação ao solo plano, os raios solares incidindo sobre uma haste vertical de 2,5 m de comprimento geram uma sombra de x m. Um pouco mais tarde, quando o ângulo de inclinação dos raios solares é de 45° graus, a mesma sombra gerada agora é de y m. A diferença ente x e y é de, aproximadamente,
sen 30° = 0,5 cos 30°= 0,866 tg 30° = 0,577
sen 45° = 0,707 cos 45°= 0,707 tg 45° = 1

Em um edifício em construção, João lança para José um
objeto amarrado a uma corda inextensível e de massa desprezível,
presa no ponto O da parede. O objeto é lançado
perpendicularmente à parede e percorre, suspenso no ar,
um arco de circunferência de diâmetro igual a 15 m, contido
em um plano horizontal e em movimento uniforme, conforme
a figura. O ponto O está sobre a mesma reta vertical
que passa pelo ponto C, ponto médio do segmento que
une João a José. O ângulo θ, formado entre a corda e o
segmento de reta OC, é constante.

Considerando senθ = 0,6, cosθ = 0,8, g = 10 m/s2 e desprezando
a resistência do ar, a velocidade angular do
objeto, em seu movimento de João a José, é igual a

Seja x um número real, 0 < x < π/2, tal que a sequência
(tan x , sec x , 2) é uma progressão aritmética (PA). Então, a
razão dessa PA é igual a
O paralelepípedo reto-retângulo ABCDEFGH representado
na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2

O seno do ângulo HÂF é igual a
O paralelepípedo reto-retângulo ABCDEFGH representado na figura, tem medida dos lados AB = 4, BC = 2 e BF = 2

O seno do ângulo HÂF é igual a
O Texto 5, em seu título faz menção a raio de sol.
Os raios do Sol incidem sobre um poste vertical e projetam
uma sombra de 5 metros de comprimento sobre uma
superfície plana. Sabendo-se que o ângulo de incidência
é de 67,5º, então, nessas condições, podemos dizer que a
altura do poste é
TEXTO 5
Raios de sol ao meio
Mais uma vez ele aparecia na minha frente como se tivesse vindo do nada. Seus olhos eram grandes e negros e pareciam ter nascido bem antes dele. Suas espinhas se agigantavam conforme o ângulo de que eram vistas. Sua orelha era algo indescritível. Além de orelha ela era disforme, meio redonda e meio achatada nas pontas. Ela era meio várias coisas. Uma orelha monstro. A boca era alguma coisa que só estava ali para cumprir seu espaço no rosto. Era boca porque estava exatamente no lugar da boca. E era a segunda vez que ele me mobilizava. Mas no conjunto de elementos díspares reinava uma sensualidade ímpar que me tirava de mim sem que eu soubesse navegar no outro que em mim surgia. De mim não sabia entender o que emanava para ele em toda a sua estranha vastidão de patologia visual. No meio sol da meia-noite as coisas se anunciaram e antes que a madrugada avançasse a lua em sua metade escondida ardeu com um olhar malicioso e sorriu.
(GONÇALVES, Aguinaldo. Das estampas. São Paulo: Nankin, 2013. p. 177.)