Carlos pretende utilizar o sistema de amortização constante (SAC), que
proporciona o pagamento da dívida em parcelas decrescentes formando
uma progressão aritmética, para financiar a compra de um imóvel no valor de R$ 300.000,00. Através de uma simulação, descobriu que o valor da
primeira parcela seria de R$ 3.642,24 e que a última parcela, de número
240, seria no valor de R$ 1.259,97. Sabendo-se que o valor do imóvel seria
100% financiado, assinale a opção que apresenta o valor total a ser pago
por Carlos, ao final do financiamento, desconsiderando-se a correção
monetária do período.




 , a progressão geométrica
, a progressão geométrica e as funções
e as funções 

 é equivalente a
é equivalente a expressão então a soma do segundo com o décimo termo dessa progressão é
expressão então a soma do segundo com o décimo termo dessa progressão é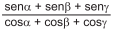 é equivalente a
é equivalente a ,
então a soma do segundo com o décimo termo dessa progressão é
,
então a soma do segundo com o décimo termo dessa progressão é