Questõessobre Progressão Aritmética - PA

InícioTodas as questões
1
1
Foram encontradas 211 questões
0967a450-75
UECE 2021 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Progressões

Sejam (x1, x2, x3, ...) uma progressão aritmética e (y1, y2, y3, ...) uma progressão geométrica, com termos positivos, tais que x1 = y1 = p. Se a razão de cada uma destas progressões é o número real positivo q, Ma é a média aritmética dos cinco primeiros termos de (x1, x2, x3, ...) e Mg é a média geométrica dos cinco primeiros termos de (y1, y2, y3, ...), então, Ma + Mg é igual a 

A
pq2 + 2q + p.
B
qp2 + 2p.
C
pq2 + p2q.
D
p + q + pq.
094f9163-75
UECE 2021 - Matemática - Progressão Aritmética - PA, Progressões

As medidas, expressas em graus, dos ângulos internos de um triângulo retângulo constituem uma progressão aritmética. Se x é a medida de um dos ângulos agudos deste triângulo, então, tg(x) pode ser igual a

A
√2/2 .
B
√3/2 .
C
√2.
D
√3.
32965118-0b
UECE 2021 - Matemática - Progressão Aritmética - PA, Progressões

No conjunto dos números reais positivos, sejam (x1, x2, x3,....) uma progressão geométrica cuja razão é o número real q e (y1, y2, y3,....) uma progressão aritmética cuja razão é r, com y1 = 3 e y5 = 7. Se para cada número inteiro positivo n, tivermos yn = log2(xn), então, é correto afirmar que o valor da soma x1 + q + r é

A
11.
B
13.
C
12.
D
14.
aff6876d-0a
UECE 2021 - Matemática - Progressão Aritmética - PA, Progressões

Se S =–1+2–3+4–5+6–7+ .... +98–99+100, então, o valor de S é igual a

A
55.
B
60.
C
50.
D
45.
0f8d94fd-04
FGV 2020 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Progressões

Um imposto progressivo sobre a renda anual do trabalhador será aplicado de acordo com a tabela:



Sérgio possui carteira assinada e recebe mensalmente R$ 7.000,00, sendo esta sua única renda. Considerando que a renda anual de Sérgio inclui a parcela do 13º salário que recebe, o valor total do imposto progressivo que terá que pagar sobre sua renda anual será de

A
R$ 16.500,00.
B
R$ 18.600,00.
C
R$ 22.200,00.
D
R$ 27.300,00.
E
R$ 34.500,00.
23f9dcad-04
CEDERJ 2021 - Matemática - Progressão Aritmética - PA, Progressões

Asequência (2x+3, 3x+4, 4x+5, ...) é uma progressão aritmética de razão 6. O quarto termo dessa progressão é

A
31.
B
33.
C
35.
D
37.
6202c363-ff
URCA 2017 - Matemática - Progressão Aritmética - PA, Progressões

Quantos termos a soma 5 + 7 + 9 + 11+ ⋯ deve ter para que o total seja 2700?

A
10
B
15
C
25
D
50
E
100
85c17520-04
ESPM 2019 - Matemática - Progressão Aritmética - PA, Progressões

As progressões aritméticas A = (3, 8, 13, 18, ...) e B = (1, 5, 9, 13, ...) têm 50 termos cada uma. O número de termos da sequência C = A ∩ B é igual a:

A
12
B
15
C
10
D
13
E
9
af6bbe7c-ff
URCA 2016 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Progressões

Se uma calculadora que custa R$100,00 hoje tiver seu preço reajustado em uma taxa composta de 2% em cada um dos próximos meses, a sequência formada por esses preços será:

A
Uma progressão geométrica de razão 1,02.
B
Uma progressão aritmética de razão 1,2.
C
Uma progressão geométrica de razão 0,02.
D
Uma progressão aritmética de razão 1,02.
E
Uma progressão geométrica de razão 1,2.
4d2ae6eb-fd
ESPM 2018 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Progressões

Seja S = (a1, a2, a3, ... , an) uma sequência de números naturais em que:

a1 = 1
a2 = 1

, para n > 2

A soma dos 50 primeiros termos dessa sequência é igual a:

A
251 – 2
B
2100 – 2
C
250 – 1
D
250
E
251
bb68ab93-f7
UEG 2016 - Matemática - Progressão Aritmética - PA, Progressão Geométrica - PG, Progressões

A sequência numérica Cn, é definida como Cn = an . bn, com n ∈ N, em que an e bn são progressões aritmética e geométrica, respectivamente. Sabendo-se que as = bs = 10 e as razões de an e bn e são iguais a 3, o termo C8 é igual a

A
100
B
520
C
1.350
D
3.800
E
5.130
4ba1c6f8-8f
UNICAMP 2021 - Matemática - Progressão Aritmética - PA, Progressões

Considere a, b, c, d termos consecutivos de uma progressão aritmética de números reais com razão r ≠ 0. Denote por D o determinante da matriz



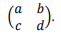
É correto afirmar que D/r² vale

A
-1
B
-2
C
-3
D
-4
4b9c0eb0-8f
UNICAMP 2021 - Matemática - Progressão Aritmética - PA, Progressões

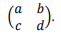
Considere que os ângulos internos de um triângulo formam uma progressão aritmética. Dado que a, b, c são as medidas dos lados do triângulo, sendo a < b < c, é correto afirmar que

A
b² + ac = a² +c²
B
a² + bc = b² +c²
C
a² - bc = b² +c²
D
b² - ac = a² +c²
62ddbc89-8e
CEDERJ 2020 - Matemática - Progressão Aritmética - PA, Progressões

Admita que cada elemento da sequência (240, x, y, z, 420, t) represente o número total de pessoas testadas e com resultado positivo para COVID durante uma semana, em cada um de 6 municípios de um determinado Estado.

Se essa sequência é uma progressão aritmética, nessa semana de testagem o número total de casos com resultados positivos nos 6 municípios foi igual a:

A
2120
B
2115
C
2110
D
2105
615689fc-76
UNIVESP 2017 - Matemática - Progressão Aritmética - PA, Progressões

Em uma progressão aritmética (P.A.), a soma dos três primeiros termos é igual a 117. Sabendo que o primeiro termo é 30, a razão dessa P.A. é

A
5
B
6
C
7
D
8
E
9
9f47e61e-5f
ENEM 2020 - Matemática - Aritmética e Problemas, Progressão Aritmética - PA, Médias, Progressões

    No Brasil, o tempo necessário para um estudante realizar sua formação até a diplomação em um curso superior, considerando os 9 anos de ensino fundamental, os 3 anos do ensino médio e os 4 anos de graduação (tempo médio), é de 16 anos. No entanto, a realidade dos brasileiros mostra que o tempo médio de estudo de pessoas acima de 14 anos é ainda muito pequeno, conforme apresentado na tabela.



    Considere que o incremento no tempo de estudo, a cada período, para essas pessoas, se mantenha constante até o ano 2050, e que se pretenda chegar ao patamar de 70% do tempo necessário à obtenção do curso superior dado anteriormente.

O ano em que o tempo médio de estudo de pessoas acima de 14 anos atingirá o percentual pretendido será 


A
2018.
B
2023.
C
2031.
D
2035.
E
2043.
c307f833-fd
UNC 2011 - Matemática - Progressão Aritmética - PA, Progressões

Em janeiro de 2010, certa indústria deu férias coletivas a seus funcionários, e a partir de fevereiro recomeçou sua produção. Considere que a cada mês essa produção cresceu em progressão aritmética, que a diferença de produção dos meses de abril e outubro de 2010 foi de 420 itens, e que em outubro a produção foi de 1120 itens.

Desta forma, pode-se concluir que o número de itens produzidos em agosto de 2010 foi:

A
⇒ 1.040
B
⇒ 910  
C
⇒ 820
D
⇒ 980
16366d16-02
UECE 2018 - Matemática - Progressão Aritmética - PA, Progressões

Se ( x1, x2, x3,﹒﹒﹒﹒ , x12, x13 ) é a progressão aritmética crescente, no intervalo [0. 2 π], tal que x1 = 0 e x13 = 2 π, então, o valor da expressão senx1.cosx2 + senx3.cosx4 + ﹒﹒﹒﹒ + senx11.cosx12 é igual a

A
√3/2.
B
-√3/2.
C
3/2.
D
-3/2.
15ff2c8e-02
UECE 2018 - Matemática - Progressão Aritmética - PA, Funções, Equações Exponenciais, Progressões

Considerando f : R → R a função definida por f(x) = 3.2x e ( x1, x2, x3,﹒﹒ ﹒, xn,﹒﹒﹒ ) uma progressão aritmética cujo primeiro termo x1 é igual a um e cuja razão é igual a -1/2 , pode-se afirmar corretamente que o valor da “soma infinita’’ f(x1) + f(x2) + f(x3) + ﹒﹒﹒﹒ + f(xn) + ﹒﹒﹒﹒ é igual a

A
8(2 + √2).
B
2(2 + √2).
C
6(2 + √2).
D
4(2 + √2).
b9da81e1-02
UNC 2017 - Matemática - Progressão Aritmética - PA, Progressões

Analise as afirmações a seguir e assinale a alternativa que contém todas as corretas.


I Uma sequência numérica é determinada conforme a lei an = n2 + 2. Essa sequência é uma progressão aritmética de razão 2.

ll Ronei contratou, durante trinta dias, um jardineiro para fazer um serviço em sua casa por 400 reais. Contudo, ao negociarem a forma de pagamento o jardineiro propôs o seguinte: em vez de R$ 400,00, gostaria de receber um pouquinho a cada dia: R$ 1,00 no primeiro dia, R$ 2,00 no segundo dia, R$ 3,00 no terceiro dia, e assim por diante, recebendo sempre a cada dia, R$ 1,00 a mais que no dia anterior. Então, ao aceitar a proposta Ronei terá um prejuízo de 65 reais.

III

A Onça e a libra são unidades de massa do sistema inglês. Sabe-se que 16 onças equivalem a uma libra. Considerando uma libra igual a 453,60 gramas, então, 128 onças equivalem a menos que 4 kg.

IV Um comerciante, visando aumentar as vendas de seu estabelecimento, fez uma promoção para determinado produto. Na compra de 4 unidades desse produto o cliente leva 5 unidades para casa. Então quando um cliente compra de oito unidades desse produto, e consequentemente leva 10 unidades para casa, estará recebendo um desconto equivalente a 25% do preço sem a promoção.

A
I - II
B
II - IV
C
II - III
D
II - III - IV