Questõessobre Problemas
Em uma escola que só tem o Ensino Fundamental II (EF2) e o Ensino Médio (EM), o número de alunos do EF2
é o dobro do número de alunos do EM. Cada aluno do EF2 possui exatamente 10 livros didáticos e cada aluno do EM possui
exatamente 14 livros didáticos.
Sabendo que o total de livros que os alunos dessa escola possuem é 3 808, o número de alunos dessa escola é
As inscrições para o vestibular de certa universidade puderam ser feitas através de 3 diferentes sites, A, B e C. Sabe-se
que A e B receberam, juntos, 1200 inscrições, que B e C
receberam, juntos, 1100 inscrições, e que A e C receberam,
juntos, 1500 inscrições. Nessas condições, é correto afirmar que o número total de inscrições para esse vestibular
foi igual a
Paulus Gerdes (1952 – 2014), matemático holandês, desenvolveu grande parte de suas pesquisas
em Moçambique. Em um de seus estudos desenvolveu uma fórmula para calcular o "peso" (P)
aproximado do gado, em quilogramas, em função do comprimento do tronco (a) e do comprimento da
cintura (b), ambos em decímetros. Pela fórmula de Gerdes, para o "peso" de um animal, multiplicamos
a medida do tronco a pelo quadrado da medida da cintura b e dividimos pelo quádruplo do número π.

Seu Bernardo, pequeno criador de gado, um pouco duvidoso da fórmula de Gerdes, pesou um de seus
garrotes na fazenda do vizinho e obteve 170 kg. Mediu o comprimento do tronco e da cintura obtendo,
respetivamente, 8,8 dm e 15 dm e, em seguida, calculou o peso do animal pela fórmula de Gerdes. Ao
comparar o peso real do animal com o peso obtido pela fórmula, ele concluiu que o erro cometido foi
de, aproximadamente:
Adote π = 3

Sofia e Flávia, estudantes do 1º ano do ensino médio, durante uma pesquisa sobre calçados solicitada pelo professor de Matemática, descobriram, dentre outras coisas, que:
• No Brasil, a fórmula 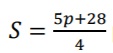 pode ser usada para calcular o número aproximado do calçado
(S) em função da medida do comprimento p do pé;
• O número do calçado na Europa é sempre 2 unidades a mais do que o número do calçado aqui
no Brasil.
pode ser usada para calcular o número aproximado do calçado
(S) em função da medida do comprimento p do pé;
• O número do calçado na Europa é sempre 2 unidades a mais do que o número do calçado aqui
no Brasil.
Depois da apresentação online dos resultados da pesquisa para a turma, elas propuseram a seguinte
situação-problema:
“O pai de Zulmira mora na Europa e lá o número do seu calçado é 42. Zulmira mora aqui no Brasil e a
medida do tamanho do seu pé é 2,4 cm a menos do que o tamanho do pé do seu pai. Qual é o número
do calçado de Zulmira em nosso país?”
A resposta correta do problema proposto por Sofia e Flávia é:
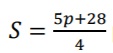 pode ser usada para calcular o número aproximado do calçado
(S) em função da medida do comprimento p do pé;
pode ser usada para calcular o número aproximado do calçado
(S) em função da medida do comprimento p do pé; Uma microempresa especializou-se em produzir um tipo de chaveiro personalizado para
brindes. O custo de produção de cada unidade é de R$ 0,42 e são comercializados em
pacotes com 400 chaveiros, que são vendidos por R$ 280,00. Além disso, essa empresa tem
um custo mensal fixo de R$ 12 800,00 que não depende do número de chaveiros produzidos.
Qual é o número mínimo de pacotes de chaveiros que devem ser vendidos mensalmente para
que essa microempresa não tenha prejuízo no mês?
Uma microempresa especializou-se em produzir um tipo de chaveiro personalizado para brindes. O custo de produção de cada unidade é de R$ 0,42 e são comercializados em pacotes com 400 chaveiros, que são vendidos por R$ 280,00. Além disso, essa empresa tem um custo mensal fixo de R$ 12 800,00 que não depende do número de chaveiros produzidos.
Qual é o número mínimo de pacotes de chaveiros que devem ser vendidos mensalmente para
que essa microempresa não tenha prejuízo no mês?
Para sua festa de 17 anos, o aniversariante convidará 132 pessoas. Ele convidará 26
mulheres a mais do que o número de homens. A empresa contratada para realizar a festa
cobrará R$ 50,00 por convidado do sexo masculino e R$ 45,00 por convidado do sexo
feminino.
Quanto esse aniversariante terá que pagar, em real, à empresa contratada, pela quantidade de
homens convidados para sua festa?
Para sua festa de 17 anos, o aniversariante convidará 132 pessoas. Ele convidará 26 mulheres a mais do que o número de homens. A empresa contratada para realizar a festa cobrará R$ 50,00 por convidado do sexo masculino e R$ 45,00 por convidado do sexo feminino.
Quanto esse aniversariante terá que pagar, em real, à empresa contratada, pela quantidade de
homens convidados para sua festa?
Segundo indicação de um veterinário, um cão de pequeno porte, nos dois primeiros
meses de vida, deverá ser alimentado diariamente com 50 g de suplemento e tomar banho
quatro vezes por mês. O dono de um cão de pequeno porte, seguindo orientações desse
veterinário, utilizou no primeiro mês os produtos/serviços de um determinado pet shop, em que
os preços estão apresentados no quadro.

No mês subsequente, o fabricante reajustou o preço do suplemento, que, nesse pet shop,
passou a custar R$ 9,00 cada pacote de 500 g. Visando manter o mesmo gasto mensal para o
dono do cão, o gerente do pet shop decidiu reduzir o preço unitário do banho. Para efeito de
cálculos, considere o mês comercial de 30 dias.
Disponível em: http://carodinheiro.blogfolha.uol.com.br. Acesso em: 20 jan. 2015 (adaptado).
Nessas condições, o valor unitário do banho, em real, passou a ser
Segundo indicação de um veterinário, um cão de pequeno porte, nos dois primeiros meses de vida, deverá ser alimentado diariamente com 50 g de suplemento e tomar banho quatro vezes por mês. O dono de um cão de pequeno porte, seguindo orientações desse veterinário, utilizou no primeiro mês os produtos/serviços de um determinado pet shop, em que os preços estão apresentados no quadro.

No mês subsequente, o fabricante reajustou o preço do suplemento, que, nesse pet shop, passou a custar R$ 9,00 cada pacote de 500 g. Visando manter o mesmo gasto mensal para o dono do cão, o gerente do pet shop decidiu reduzir o preço unitário do banho. Para efeito de cálculos, considere o mês comercial de 30 dias.
Disponível em: http://carodinheiro.blogfolha.uol.com.br. Acesso em: 20 jan. 2015 (adaptado).
Nessas condições, o valor unitário do banho, em real, passou a ser
O Índice de Desenvolvimento da Educação Básica (Ideb), criado para medir a qualidade
do aprendizado do ensino básico no Brasil, é calculado a cada dois anos. No seu cálculo são
combinados dois indicadores: o aprendizado e o fluxo escolar, obtidos a partir do Censo
Escolar e das avaliações oficiais promovidas pelo Inep.
O Ideb de uma escola numa dada série escolar pode ser calculado pela expressão
Ideb = N x P,
em que N é a média da proficiência em língua portuguesa e matemática, obtida a partir do
Sistema de Avaliação da Educação Básica (Saeb), e variando de 0 a 10. O indicador P, que
varia de 0 a 1, por sua vez, refere-se ao fluxo escolar, pois considera as taxas de aprovação e
reprovação da instituição, sendo calculado por
P = 1/T,
em que T é o tempo médio de permanência dos alunos na série.
Disponível em: www.inep.gov.br. Acesso em: 2 ago. 2012.
Uma escola apresentou no 9º ano do ensino fundamental, em 2017, um Ideb diferente
daquele que havia apresentado nessa mesma série em 2015, pois o tempo médio de
permanência dos alunos no 9º ano diminuiu 2%, enquanto a média de proficiência em língua
portuguesa e matemática, nessa série, aumentou em 2%.
Dessa forma, o Ideb do 9º ano do ensino fundamental dessa escola em 2017, em relação ao
calculado em 2015,
O Índice de Desenvolvimento da Educação Básica (Ideb), criado para medir a qualidade do aprendizado do ensino básico no Brasil, é calculado a cada dois anos. No seu cálculo são combinados dois indicadores: o aprendizado e o fluxo escolar, obtidos a partir do Censo Escolar e das avaliações oficiais promovidas pelo Inep.
O Ideb de uma escola numa dada série escolar pode ser calculado pela expressão
Ideb = N x P,
em que N é a média da proficiência em língua portuguesa e matemática, obtida a partir do Sistema de Avaliação da Educação Básica (Saeb), e variando de 0 a 10. O indicador P, que varia de 0 a 1, por sua vez, refere-se ao fluxo escolar, pois considera as taxas de aprovação e reprovação da instituição, sendo calculado por
P = 1/T,
em que T é o tempo médio de permanência dos alunos na série.
Disponível em: www.inep.gov.br. Acesso em: 2 ago. 2012.
Uma escola apresentou no 9º ano do ensino fundamental, em 2017, um Ideb diferente daquele que havia apresentado nessa mesma série em 2015, pois o tempo médio de permanência dos alunos no 9º ano diminuiu 2%, enquanto a média de proficiência em língua portuguesa e matemática, nessa série, aumentou em 2%.
Dessa forma, o Ideb do 9º ano do ensino fundamental dessa escola em 2017, em relação ao calculado em 2015,
“1, 2, 3, GOL, 5, 6, 7, GOL, 9, 10, 11, GOL, 13, GOL, 15, GOL, 17, 18, 19, GOL, 21, 22, 23,
GOL, 25, ...”
Para a Copa do Mundo de Futebol de 2014, um bar onde se reuniam amigos para assistir
aos jogos criou uma brincadeira. Um dos presentes era escolhido e tinha que dizer, numa
sequência em ordem crescente, os números naturais não nulos, trocando os múltiplos de 4 e
os números terminados em 4 pela palavra GOL. A brincadeira acabava quando o participante
errava um termo da sequência.
Um dos participantes conseguiu falar até o número 103, respeitando as regras da
brincadeira.
O total de vezes em que esse participante disse a palavra GOL foi
“1, 2, 3, GOL, 5, 6, 7, GOL, 9, 10, 11, GOL, 13, GOL, 15, GOL, 17, 18, 19, GOL, 21, 22, 23, GOL, 25, ...”
Para a Copa do Mundo de Futebol de 2014, um bar onde se reuniam amigos para assistir aos jogos criou uma brincadeira. Um dos presentes era escolhido e tinha que dizer, numa sequência em ordem crescente, os números naturais não nulos, trocando os múltiplos de 4 e os números terminados em 4 pela palavra GOL. A brincadeira acabava quando o participante errava um termo da sequência.
Um dos participantes conseguiu falar até o número 103, respeitando as regras da brincadeira.
O total de vezes em que esse participante disse a palavra GOL foi
Um agricultor sabe que a colheita da safra de soja será concluída em 120 dias caso
utilize, durante 10 horas por dia, 20 máquinas de um modelo antigo, que colhem 2 hectares por
hora. Com o objetivo de diminuir o tempo de colheita, esse agricultor optou por utilizar
máquinas de um novo modelo, que operam 12 horas por dia e colhem 4 hectares por hora.
Quantas máquinas do novo modelo ele necessita adquirir para que consiga efetuar a colheita
da safra em 100 dias?
Um agricultor sabe que a colheita da safra de soja será concluída em 120 dias caso utilize, durante 10 horas por dia, 20 máquinas de um modelo antigo, que colhem 2 hectares por hora. Com o objetivo de diminuir o tempo de colheita, esse agricultor optou por utilizar máquinas de um novo modelo, que operam 12 horas por dia e colhem 4 hectares por hora.
Quantas máquinas do novo modelo ele necessita adquirir para que consiga efetuar a colheita
da safra em 100 dias?
Na última eleição para a presidência de um clube, duas chapas se inscreveram (I e II). Há
dois tipos de sócio: patrimoniais e contribuintes. Votos de sócios patrimoniais têm peso 0,6 e
de sócios contribuintes têm peso 0,4. A chapa I recebeu 850 votos de sócios patrimoniais e 4
300 de sócios contribuintes; a chapa II recebeu 1 300 votos de sócios patrimoniais e 2 120 de
sócios contribuintes. Não houve abstenções, votos em branco ou nulos, e a chapa I foi
vencedora. Haverá uma nova eleição para a presidência do clube, com o mesmo número e
tipos de sócios, e as mesmas chapas da eleição anterior. Uma consulta feita pela chapa II
mostrou que os sócios patrimoniais não mudarão seus votos, e que pode contar com os votos
dos sócios contribuintes da última eleição. Assim, para que vença, será necessária uma
campanha junto aos sócios contribuintes com o objetivo de que mudem seus votos para a
chapa II.
A menor quantidade de sócios contribuintes que precisam trocar seu voto da chapa I para a
chapa II para que esta seja vencedora é
Na última eleição para a presidência de um clube, duas chapas se inscreveram (I e II). Há dois tipos de sócio: patrimoniais e contribuintes. Votos de sócios patrimoniais têm peso 0,6 e de sócios contribuintes têm peso 0,4. A chapa I recebeu 850 votos de sócios patrimoniais e 4 300 de sócios contribuintes; a chapa II recebeu 1 300 votos de sócios patrimoniais e 2 120 de sócios contribuintes. Não houve abstenções, votos em branco ou nulos, e a chapa I foi vencedora. Haverá uma nova eleição para a presidência do clube, com o mesmo número e tipos de sócios, e as mesmas chapas da eleição anterior. Uma consulta feita pela chapa II mostrou que os sócios patrimoniais não mudarão seus votos, e que pode contar com os votos dos sócios contribuintes da última eleição. Assim, para que vença, será necessária uma campanha junto aos sócios contribuintes com o objetivo de que mudem seus votos para a chapa II.
A menor quantidade de sócios contribuintes que precisam trocar seu voto da chapa I para a
chapa II para que esta seja vencedora é
Uma casa de dois andares está sendo projetada. É necessário incluir no projeto a construção de uma escada para o acesso ao segundo andar. Para o cálculo das dimensões dos degraus utilizam-se as regras:
|2h + b - 63,5| ≤ 1,5 e 16 ≤ h ≤ 19,
nas quais h é a altura do degrau (denominada espelho) e b é a profundidade da pisada, como mostra a figura. Por conveniência, escolheu-se a altura do degrau como sendo h = 16. As unidades de h e b estão em centímetro.

Nesse caso, o mais amplo intervalo numérico ao qual a
profundidade da pisada (b) deve pertencer, para que as
regras sejam satisfeitas é

Muitos modelos atuais de veículos possuem
computador de bordo. Os computadores informam em
uma tela diversas variações de grandezas associadas
ao desempenho do carro, dentre elas o consumo médio
de combustível. Um veiculo, de um determinado modelo,
pode vir munido de um dos dois tipos de computadores
de bordo:
• Tipo A: informa a quantidade X de litro de
combustível gasto para percorrer 100 quilômetros;
• Tipo B: informa a quantidade de quilômetro que
o veiculo é capaz de percorrer com um litro de
combustível.
Um veiculo utiliza o computador do Tipo A, e ao final
de uma viagem o condutor viu apresentada na tela a
informação “X/100”.
Caso o seu veículo utilizasse o computador do Tipo B, o
valor informado na tela seria obtido pela operação
O fenômeno das manifestações populares de massa traz à discussão como estimar o número de pessoas
presentes nesse tipo de evento. Uma metodologia usada é: no momento do ápice do evento, é feita uma foto aérea
da via pública principal na área ocupada, bem como das vias afluentes que apresentem aglomerações de pessoas
que acessam a via principal. A foto é sobreposta por um mapa virtual das vias, ambos na mesma escala, fazendo-se
um esboço geométrico da situação. Em seguida, subdivide-se o espaço total em trechos, quantificando a densidade,
da seguinte forma:
• 4 pessoas por metro quadrado, se elas estiverem andando em uma mesma direção;
• 5 pessoas por metro quadrado, se elas estiverem se movimentando sem deixar o local;
• 6 pessoas por metro quadrado, se elas estiverem paradas.
É feito, então, o cálculo do total de pessoas, considerando os diversos trechos, e desconta-se daí 1 000 pessoas
para cada carro de som fotografado.
Com essa metodologia, procederam-se aos cálculos para estimar o número de participantes na manifestação cujo
esboço geométrico é dado na figura. Há três trechos na via principal: MN, NO e OP, e um trecho numa via afluente
da principal: QR .

Obs.: a figura não está em escala (considere as medidas dadas).
Segundo a metodologia descrita, o número estimado de pessoas presentes a essa manifestação foi igual a

Um hotel de 3 andares está sendo construído. Cada
andar terá 100 quartos. Os quartos serão numerados de
100 a 399 e cada um terá seu número afixado à porta.
Cada número será composto por peças individuais, cada
uma simbolizando um único algarismo.
Qual a quantidade mínima de peças, simbolizando o
algarismo 2, necessárias para identificar o número de
todos os quartos?
Um grupo sanguíneo, ou tipo sanguíneo, baseia-se na
presença ou ausência de dois antígenos, A e B, na superfície
das células vermelhas do sangue. Como dois antígenos
estão envolvidos, os quatro tipos sanguíneos distintos são:
• Tipo A: apenas o antígeno A está presente;
• Tipo B: apenas o antígeno B está presente;
• Tipo AB: ambos os antígenos estão presentes;
• Tipo O: nenhum dos antígenos está presente.
Disponível em; http://saude.hsw.uol.com.br. Acesso em: 15 abr. 2012 (adaptado).
Foram coletadas amostras de sangue de 200 pessoas
e, após análise laboratorial, foi identificado que em 100
amostras está presente o antígeno A, em 110 amostras
há presença do antígeno B e em 20 amostras nenhum
dos antígenos está presente.
Dessas pessoas que foram submetidas à coleta de
sangue, o número das que possuem o tipo sanguíneo A
é igual a
Uma artesã fabrica chaveiros
com produtos recicláveis, possuindo
um custo fixo mensal de R$ 400,00, sendo que o custo variável por peça
seja de R$3,00 e a venda de cada
unidade tem valor de R$ 12,00.
Considerando que x seja a
quantidade de peças vendidas em
um mês, quantas peças essa artesã
deve vender em mês para que seu
lucro seja de R$ 1400,00?
As novas tecnologias de
informação e comunicação vem
ajudando a comunidade médica a
informar a população sobre métodos
de prevenção de várias doenças. Um
estudo realizado por um grupo de
médicos permitiu identificar que na
região sudeste doenças
relacionadas a falta de higiene
sofrerão reduções sucessivas de
10% no ano de 2020, 12% no ano de
2021 e 14% no ano de 2022, essas
reduções são justificadas através de
campanhas em rádio, TV, internet,
jornais e revistas. Dentro dessa
perspectiva, pode-se afirmar que a
redução total dessas doenças ao
longo dos três anos corresponde a
aproximadamente:
O Sr. Fernando comprou um terreno retangular que mede 18 metros de largura por 30 metros de
comprimento. Para cercar completamente sua propriedade, ele comprou estacas de madeira e rolos de
arame farpado. A pessoa contratada para fazer o serviço sugeriu que fossem colocados cinco fios de arame
contornando todo o perímetro, conforme a FIGURA 2.
 Fernando acatou a sugestão. Sabendo que o arame farpado é vendido em rolos de 50 metros, determine
quantos rolos, no mínimo, serão comprados.
Fernando acatou a sugestão. Sabendo que o arame farpado é vendido em rolos de 50 metros, determine
quantos rolos, no mínimo, serão comprados.
