O gerente de uma empresa sabe que 70% de seus
funcionários são do sexo masculino e foi informado de
que a porcentagem de empregados fumantes nessa
empresa é de 5% dos homens e de 5% das mulheres.
Selecionando, ao acaso, a ficha de cadastro de um dos
funcionários, verificou tratar-se de um fumante.
Qual a probabilidade de esse funcionário ser do sexo
feminino?
O gerente de uma empresa sabe que 70% de seus funcionários são do sexo masculino e foi informado de que a porcentagem de empregados fumantes nessa empresa é de 5% dos homens e de 5% das mulheres. Selecionando, ao acaso, a ficha de cadastro de um dos funcionários, verificou tratar-se de um fumante.
Qual a probabilidade de esse funcionário ser do sexo feminino?








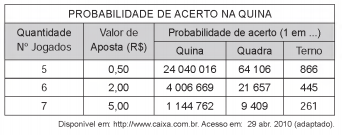
 o que mostra que Antônio tem mais chances
3114
de acertar.
o que mostra que Antônio tem mais chances
3114
de acertar. o que mostra que Antônio tem mais chances de acertar.
o que mostra que Antônio tem mais chances de acertar. o que mostra que José tem mais chances de acertar.
o que mostra que José tem mais chances de acertar. o que mostra que Antônio tem mais chances de acertar.
o que mostra que Antônio tem mais chances de acertar. o que mostra que José tem mais chances de acertar.
o que mostra que José tem mais chances de acertar.