Questõessobre Pontos e Retas
O conjunto dos números complexos z = a + bi com a,b reais e i = √-1 possui como operações a adição
(a + bi) + (c + di) = (a + c) + (b + d)i e o produto (a + bi) ∙ (c + di) = (ac - bd) + (ad + bc)i.
Esses números possuem grande diversidade de aplicações, desde o entendimento da existência de
buracos negros no universo até o uso em computação gráfica. Nesse último caso, trabalhando as
operações descritas, pode-se transladar, ampliar ou reduzir e rotacionar fi guras na tela do computador.
Dados os números z1 = 2 + i; z2
= -1 + 2i e z3 = -2 - 2i, obtém-se o seguinte triângulo:

Considerando o triângulo dado, utilizando as operações de multiplicação e adição, nessa ordem, pelo
número z = 1 - 2i obteremos a fi gura:





O ponto A(3, 4) pertence a uma circunferência
λ cujo centro tem abscissa 7 e ordenada inteira.
Uma reta r passa pelo ponto O(0, 0) e pelo ponto
A e a distância de r até o centro de λ é igual a 2. O
raio da circunferência λ é
Uma circunferência tangencia o lado BC de um
triângulo ABC no ponto F e intersecta os lados
AB e AC desse triângulo, nos pontos E e D
respectivamente, conforme mostra a figura.

Sabendo que essa circunferência passa pelo
ponto A, a distância entre os pontos D e E, em
cm, é igual a
Uma circunferência tangencia o lado BC de um triângulo ABC no ponto F e intersecta os lados AB e AC desse triângulo, nos pontos E e D respectivamente, conforme mostra a figura.

Sabendo que essa circunferência passa pelo
ponto A, a distância entre os pontos D e E, em
cm, é igual a
Um grupo de escoteiros resolveu montar o
acampamento de tal forma que foram armadas três
grandes barracas, as quais ficaram equidistantes de um
ponto onde se localizava a fogueira. Para tanto, as
barracas foram distribuídas usando um plano cartesiano
como referência. Sabendo que as barracas estavam localizadas
nos pontos H(1;3), I(1;1) e J(4;1), em qual ponto desse
plano cartesiano está localizada a fogueira?
Seja r uma reta com equação r: 3x + 2y = 20.
Uma reta s a intercepta no ponto (2,7).
Sabendo que r e s são perpendiculares entre si,
qual é a equação da reta s?
Na figura abaixo, o segmento AB é a hipotenusa
de um triângulo retângulo isósceles ACB, retângulo em
C, e mede 4√2.

Sabendo que as coordenadas do ponto A são
(-1,1), e que a abscissa do ponto C é positiva, as
coordenadas de C são:

Duas retas perpendiculares se cortam no ponto (2, 5) e são definidas pelas equações y = ax + 1 e y = bx + c. Com
base nessas informações, é correto afirmar que o valor do coeficiente linear c é igual a:
Considere que os quarteirões de um bairro tenham sido
desenhados no sistema cartesiano, sendo a origem o
cruzamento das duas ruas mais movimentadas desse bairro.
Nesse desenho, as ruas têm suas larguras desconsideradas e
todos os quarteirões são quadrados de mesma área e a
medida de seu lado é a unidade do sistema.
A seguir, há uma representação dessa situação, em que os
pontos A, B, C e D representam estabelecimentos comerciais
desse bairro.

Suponha que uma estação de rádio comunitária, de fraco sinal,
garante área de cobertura para todo estabelecimento que se
encontra num ponto cujas coordenadas satisfaçam à
inequação:

A fim de avaliar a qualidade do sinal e proporcionar uma futura
melhora, a assistência técnica da rádio realizou uma inspeção
para saber quais estabelecimentos estavam dentro da área de
cobertura, pois estes conseguem ouvir a rádio, enquanto os
outros não.
Os estabelecimentos que conseguem ouvir a rádio são apenas:
Considere que os quarteirões de um bairro tenham sido desenhados no sistema cartesiano, sendo a origem o cruzamento das duas ruas mais movimentadas desse bairro. Nesse desenho, as ruas têm suas larguras desconsideradas e todos os quarteirões são quadrados de mesma área e a medida de seu lado é a unidade do sistema.
A seguir, há uma representação dessa situação, em que os pontos A, B, C e D representam estabelecimentos comerciais desse bairro.

Suponha que uma estação de rádio comunitária, de fraco sinal, garante área de cobertura para todo estabelecimento que se encontra num ponto cujas coordenadas satisfaçam à inequação:

A fim de avaliar a qualidade do sinal e proporcionar uma futura melhora, a assistência técnica da rádio realizou uma inspeção para saber quais estabelecimentos estavam dentro da área de cobertura, pois estes conseguem ouvir a rádio, enquanto os outros não.
Os estabelecimentos que conseguem ouvir a rádio são apenas:
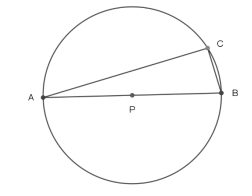
Na figura abaixo, o ângulo 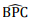 mede π/6 radianos, e o ponto é o centro da
circunferência de raio 3. A área do triângulo ABC, em unidades de área, é
mede π/6 radianos, e o ponto é o centro da
circunferência de raio 3. A área do triângulo ABC, em unidades de área, é
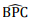 mede π/6 radianos, e o ponto é o centro da
circunferência de raio 3. A área do triângulo ABC, em unidades de área, é
mede π/6 radianos, e o ponto é o centro da
circunferência de raio 3. A área do triângulo ABC, em unidades de área, é 
Considere a reta de equação y = 2x e a parábola de equação y = x2 - 3x + 6 . Sejam ( x0 , y0) e ( x1, y1) os
pontos de interseção entre a reta e a parábola.
Quanto vale x0 + x1?
Considere o quadrado ABCD. O ponto E é o ponto médio do lado AB. O ponto F é o ponto médio do lado AD e o
ponto G é o ponto médio do segmento AF.
Seja θ = AEG
Quanto vale
cos(θ)?


√3/2
Para o controle e ajustes de engrenagens do maquinário de uma fábrica, é indispensável determinar todos
os ângulos para verificar tensões em seus pontos de sustentação.
Este sistema indica pontos de sustentação e ângulos que os técnicos encontraram durante a manutenção
de um maquinário.

Sabendo que as retas (r) e (s) são paralelas, o valor da medida do ângulo a, em graus, é:

Neste gráfico estão representadas as retas (r), (s) e (t).

Sabendo que as retas (r) e (s) são paralelas e que as retas (r) e (t) são perpendiculares, a equação dareta (s) é:

Quatro pessoas estão posicionadas em pontos distintos A, B, C e D, como pode ser observado nesta figura.
As quatro pessoas resolveram se encontrar em um dos pontos A, B, C e D. Para esse encontro, a pessoa
que está no ponto escolhido permanecerá parada enquanto as outras três pessoas se deslocam em linha
reta até o ponto de encontro.
O ponto de encontro será escolhido de forma que a soma das distâncias percorridas pelas três pessoas
seja mínima.

Considerando as condições propostas, o ponto de encontro das quatro pessoas será:

Sejam
A(1,a), B(b,3), C(4,6) e
D(1,5) os vértices de um paralelogramo e  , o ponto
médio da diagonal
AC. O produto
a . b
é igual a:
, o ponto
médio da diagonal
AC. O produto
a . b
é igual a:
 , o ponto
médio da diagonal
AC. O produto
a . b
é igual a:
, o ponto
médio da diagonal
AC. O produto
a . b
é igual a: 

A Figura 1 representa a visão frontal de um cubo de aresta de 24 cm sobre um plano α e
cortado por um plano β .

FIGURA 1: Vista frontal do cubo cortado pelo plano β
Sabendo que o ângulo formado entre os planos α e β é igual a 30 graus, e que a distância
entre a reta r de interseção dos dois planos e a aresta do cubo paralela a r mais próxima de r é
de 10 cm, então o volume da parte do cubo compreendida entre os dois planos é:



Em um plano cartesiano, o ponto C (2, 3) é o centro de umacircunferência de raio √2. O ponto P, de ordenada 4, pertence à circunferência, e a reta r, que passa pelos pontos P e C,
intersecta os eixos coordenados nos pontos R e S, conforme
mostra a figura.

Sabendo que o segmento  está contido no 1o
quadrante, a
distância entre os pontos R e S é
está contido no 1o
quadrante, a
distância entre os pontos R e S é
Em um plano cartesiano, o ponto C (2, 3) é o centro de umacircunferência de raio √2. O ponto P, de ordenada 4, pertence à circunferência, e a reta r, que passa pelos pontos P e C, intersecta os eixos coordenados nos pontos R e S, conforme mostra a figura.

Sabendo que o segmento  está contido no 1o
quadrante, a
distância entre os pontos R e S é
está contido no 1o
quadrante, a
distância entre os pontos R e S é