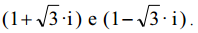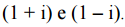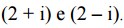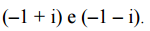1bd98c8d-b9
UNESP 2019 - Matemática - Polinômios
Considere os polinômios 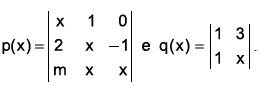
Para que p(x) seja divisível por q(x), é necessário que m seja
igual a
Considere os polinômios 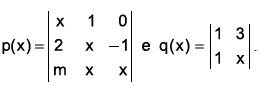
Para que p(x) seja divisível por q(x), é necessário que m seja
igual a
A
30.
B
12.
C
–12.
D
–3.
E
–30.