Assinale a proposição CORRETA.
A soma dos coeficientes do binômio
(2a - 3b)5 é 1.
Assinale a proposição CORRETA.
A soma dos coeficientes do binômio
(2a - 3b)5 é 1.

Assinale a proposição CORRETA.
A soma dos coeficientes do binômio
(2a - 3b)5 é 1.

1.
Em uma maratona de conhecimentos, o vencedor da prova sobre expressões algébricas encontrou corretamente o resto da divisão do polinômio x10 + x9 + x8 +... + x - 9 por x2 − 1.
Esse resto é
Considere o polinômio p(x) = x3 − 8x2 + 19x − 12.
A soma dos quadrados das raízes desse polinômio é
I. O coeficiente de x6 em P(x) é zero.
II. x = 0 é raiz de Q(x).
III. x = 2 é raiz de P(x).
IV. O resto da divisão de P(x) por Q(x) é um polinômio de grau 2.
Dadas as matrizes:

O quociente da divisão do polinômio p(x) = determinante (A - Ix) pelo polinômio q(x) = x − 2 é:
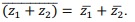 .
. Considere o polinômio p definido por p(x) = x2 + 2(n + 2)x + 9n .
Se as raízes de p(x) = 0 são iguais, os valores de n são