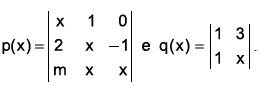Questõessobre Polinômios

InícioTodas as questões
1
1
Foram encontradas 209 questões
3dd7c097-d8
UEA 2019 - Matemática - Matrizes, Álgebra Linear, Polinômios

Seja o polinômio p(x) obtido pelo determinante da matriz


Para que a equação p(x) = 0 tenha uma única raiz real, o valor de m deverá ser

A
–3.
B
–2.
C
–1.
D
2.
E
0.
1888e08b-d8
INSPER 2015 - Matemática - Polinômios

Considere um polinômio P(x) do 4° grau, de coeficientes reais, tal que:


  2. -P(-3) = P(1) = P(5) = 0;
  3. -P(0) e P(2) são, ambos, números positivos.


Nessas condições, os sinais dos números P(-5), P(4) e P(6), são, respectivamente,

A
positivo, negativo e negativo.
B
positivo, negativo e positivo.
C
negativo, negativo e negativo.
D
negativo, positivo e negativo.
E
negativo, positivo e positivo.
a651dcfc-d8
IFF 2016 - Matemática - Polinômios

Sabendo que P(x)=m⋅x3 – 6x+w , que P(0) = 1 e P(3) = 37, então m + w é:

A
2.
B
1.
C
3.
D
1/33.
E
55/27.
e91e96b6-d7
FAMERP 2016 - Matemática - Polinômios

A figura mostra os gráficos de duas funções polinomiais do 1° grau, f e g, num mesmo sistema cartesiano ortogonal, sendo que o gráfico de f passa pela origem.



Sabendo-se que f(5) = g(5) e g(f(0)) = 14, é correto afirmar que g(6) é igual a

A
36/5
B
7
C
37/5
D
34/5
E
32/5
9950928e-d7
FAMERP 2017 - Matemática - Polinômios

Sabendo-se que uma das raízes da equação algébrica 2x3 – 3x2 – 72x – 35 = 0 é -1/2, a soma das outras duas raízes é igual a

A
-3.
B
3.
C
-2.
D
1.
E
2.
9949807a-d7
FAMERP 2017 - Matemática - Polinômios

As figuras indicam uma sequência de empilhamentos de cubos de 1 cm3. Da primeira pilha em diante, os volumes das pilhas, em cm3, são iguais a 1, 5, 14, 30, 55, e assim sucessivamente.


Sabe-se que a soma 1 + 22 + 32 + 42 + 52 + ... + x2 é um polinômio do terceiro grau, dado por P(x) = mx3 + nx2 + px, com m, n e p racionais. Portanto, P(1) = 1, P(2) = 5, P(3) = 14, P(4) = 30 e assim por diante. Nas condições dadas, m é igual a

A
1/2
B
5/6
C
2/3
D
1/6
E
1/3
2dc13e2d-d8
FGV 2014 - Matemática - Polinômios

Seja P(m n, )o ponto pertencente à circunferência de equação x2+y2-6x-4y+12=0 e que tem ordenada mínima. O produto m.n vale:

A
2
B
2,25
C
2,5
D
2,75
E
3
f8a78493-d7
FAMERP 2018 - Matemática - Polinômios

O gráfico de uma função polinomial do 1º grau f: ℝ → ℝ, dada por f(x) = ax + b, é uma reta de coeficiente angular positivo. Sabe-se ainda que f(f(x)) = 25x + 9. Assim, a intersecção do gráfico de f com o eixo y se dá em um ponto de ordenada

A
4/3
B
5/3
C
1/2
D
-4/3
E
3/2
fd6d6a52-b4
UEFS 2010 - Matemática - Polinômios

Sendo α, β e γ raízes da equação x3 +4x2 −6x+3=0, é verdade que tg[(1/α + 1/β + 1/y) π/3] é igual a

A
√3/3
B
1
C
0
D
-√3
E
-2√3
54191e39-b1
UFRR 2016 - Matemática - Polinômios

Sejam P1 (x) = x³ + x² - x - 1 e P2 (x) = x³ + 3x² + 3x +1 polinômios tais que α é raiz real de P1 (x). Então P2 (α) é igual a

A
10 ou 13;
B
9 ou 7;
C
8 ou 0;
D
11 ou 20;
E
12 ou 19.
c0bf03e4-c9
URCA 2019 - Matemática - Polinômios

Analiticamente a equação 4x² - 9y² - 8x +y -36 y =0 representa:

A
Uma Elipse
B
Uma circunferência
C
Um par de retas concorrentes
D
Uma hipérbole
E
Um par de retas paralelas
c0b112fd-c9
URCA 2019 - Matemática - Polinômios

Determine o módulo da diferença entre as raízes reais da equação ( x-4)4 + (x-2)4 = 82.

A
6
B
5
C
4
D
7
E
8
880027d3-cb
IF-PR 2017 - Matemática - Polinômios

A expressão algébrica 4x + xy/4y + y² - 42x²zy²/63zxy³ com x ≠ 0, y ≠ 0 e z ≠ 0 , equivale a:

A
0.
B
12xy/7z.
C
- 7x/6y.
D
x/3y.
49ea8023-bc
UNEB 2013 - Matemática - Polinômios

Ao desmontar um cubo de Rubik (cubo mágico), uma criança percebeu que ele era formado por vinte e sete cubinhos menores e que dentre esses existiam oito cubinhos com três faces pintadas, doze com apenas duas faces pintadas, seis com apenas uma das faces pintadas e apenas um cubinho não possuía nenhuma das faces pintadas.

A tabela a seguir, mostra o número de cubinhos, de cada tipo, que podem ser obtidos ao dividir a aresta de um cubo de madeira pintado, em partes iguais.



Nessas condições, pode-se afirmar que, em R, a soma dos inversos das raízes do polinômio P(x) = P3(x) − P1(x) + P2(x) é igual a

A
1/4
B
1/2
C
3/5
D
2/3
E
4/5
09c6a655-bb
UECE 2014 - Matemática - Polinômios

A equação x5 – x = 0 possui

A
cinco soluções reais.
B
três soluções reais e duas complexas não reais.
C
uma solução real e quatro complexas não reais.
D
quatro soluções reais e uma complexa não real.
09b29042-bb
UECE 2014 - Matemática - Polinômios

Se m, p e q são as raízes da equação 6x3 – 11x2 + 6x – 1 = 0, então o resultado da divisão da soma m + p + q pelo produto m.p.q é

A
13.
B
11.
C
17.
D
15.
1bd98c8d-b9
UNESP 2019 - Matemática - Polinômios

Considere os polinômios  



Para que p(x) seja divisível por q(x), é necessário que m seja igual a

A
30.
B
12.
C
–12.
D
–3.
E
–30.
0aef3fc4-c8
UFSC 2011 - Matemática - Polinômios

Assinale a proposição CORRETA.


O resto da divisão do polinômio P(x) = x72 + 3x60 - 2x15 + x10 - 2x5 +1 por Q (x) = x + 1 é 10.

C
Certo
E
Errado
0ae98f88-c8
UFSC 2011 - Matemática - Polinômios

Assinale a proposição CORRETA.


O polinômio P(x) = x15 - 3x3 + 3x2 - x + 1 admite pelo menos uma raiz real.

C
Certo
E
Errado
a75b19cd-cd
SEBRAE - SP 2019 - Matemática - Polinômios

Dado o polinômio de grau 2 descrito por p(x) = ax2 − 4x + b − 3, em que a e b são números reais, se p(2) = 4 e 1 é raiz desse polinômio, então os valores de a e b são:

A
a = 8/3 e b = 29/3.
B
a = 8/3 e b = 53/8.
C
a = −8/3 e b = 29/3.
D
a = 22/5 e b = 13/5.
E
a = −22/5 e b = 57/5.