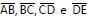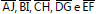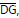968c7254-e6
Esamc 2016 - Matemática - Áreas e Perímetros, Polígonos, Geometria Plana
Um procedimento utilizado para o cálculo de áreas de polígonos não
regulares é a soma das áreas de triângulos não-sobrepostos internos
ao polígono cuja reunião seja equivalente ao próprio polígono. Nesses
casos, é de grande valia a utilização da “fórmula de Herão”, dada por A = √ S.(s - a) . (s - b) . (s - c) em que s = a + b +c/2 que determina a
área A do triângulo cujos lados medem a, b e c.
Utilizando o procedimento descrito acima, pode-se afirmar que a área
(em m²) da figura abaixo, construída fora de escala, pertence a qual
dos intervalos?

Um procedimento utilizado para o cálculo de áreas de polígonos não
regulares é a soma das áreas de triângulos não-sobrepostos internos
ao polígono cuja reunião seja equivalente ao próprio polígono. Nesses
casos, é de grande valia a utilização da “fórmula de Herão”, dada por A = √ S.(s - a) . (s - b) . (s - c) em que s = a + b +c/2 que determina a
área A do triângulo cujos lados medem a, b e c.
Utilizando o procedimento descrito acima, pode-se afirmar que a área
(em m²) da figura abaixo, construída fora de escala, pertence a qual
dos intervalos?

A
[9,18]
B
]18,27]
C
]27, 36]
D
]36, 45]
E
]45, 54]
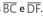 .
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
.
Se BE = 2; CE, EF = 2; DE, AB = 4 cm e
AD = 9 cm, qual das medidas a seguir
mais se aproxima de CF?
 do quadrado, é
igual a:
do quadrado, é
igual a:



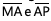 são congruentes e os segmentos
são congruentes e os segmentos 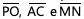 são paralelos. A
diferença entre as medidas dos segmentos
são paralelos. A
diferença entre as medidas dos segmentos 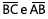 é igual a:
é igual a: