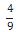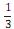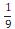O Museu do Louvre, localizado em Paris, na França,
é um dos museus mais visitados do mundo. Uma de
suas atrações é a Pirâmide de Vidro, construída no final
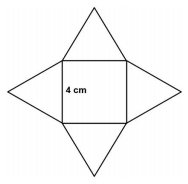
da década de 1980. A seguir tem-se, na Figura 1, uma
foto da Pirâmide de Vidro do Louvre e, na Figura 2, uma
pirâmide reta de base quadrada que a ilustra.

Considere os pontos A, B, C, D como na Figura 2.
Suponha que alguns reparos devem ser efetuados
na pirâmide. Para isso, uma pessoa fará o seguinte
deslocamento: 1) partir do ponto A e ir até o ponto B,
deslocando-se pela aresta AB; 2) ir de B até C, deslocandose
pela aresta que contém esses dois pontos; 3) ir de C até D, pelo caminho de menor comprimento; 4) deslocar-se de D até B pela aresta que contém esses dois pontos.
Disponível em: http://viagenslacoste.blogspot.com. Acesso em: 29 fev. 2012.
A projeção do trajeto da pessoa no plano da base da
pirâmide é melhor representada por








 são cevianas, perpendiculares em R, do triângulo
ABC, com AP = CQ = 4 cm;
são cevianas, perpendiculares em R, do triângulo
ABC, com AP = CQ = 4 cm;