Questões sobre Pirâmides | Pratique com o Prisma

e406cb28-de

Unimontes - MG 2019 - Matemática - Pirâmides, Geometria Espacial

Uma pirâmide tem 4 m de altura e 160 m3 de volume. Paralelamente a sua base e a 2 m de seu vértice, traça-se um plano que a divide em uma pirâmide menor e um tronco de pirâmide. O volume, em m3 , do tronco dessa pirâmide é igual a

A

140.

B

100.

C

80.

D

20.

2f7912a8-e5

UFCG 2009, UFCG 2009 - Matemática - Aritmética e Problemas, Pirâmides, Razão, Proporção e Números Proporcionais, Geometria Espacial

Em homenagem ao Ano Internacional da Matemática, um artista propôs a construção de uma pirâmide posicionada sobre um hemisfério. A base da pirâmide é um quadrado inscrito no círculo da base do hemisfério, como pode ser visto na figura abaixo. Se o volume da parte esférica e o volume da parte em forma de pirâmide são iguais, qual a razão entre o comprimento da aresta da base da pirâmide e a altura da pirâmide?

A

π/2

B

C

√2/π

D

√π/3

E

3/2

5896c2fa-d7

MACKENZIE 2010 - Matemática - Pirâmides, Geometria Espacial

A figura representa um bloco com formato de um cubo de aresta a , do qual é retirada uma pirâmide. Se A, B e C são pontos médios dos lados do cubo e se o volume da peça restante é igual a 188/3, o valor de a2 + a é

A

16

B

4

C

20

D

28

E

8

d7ec4e8a-d8

FAMERP 2015 - Matemática - Pirâmides, Geometria Espacial

A figura representa uma pirâmide com base quadrada ABCD de lado x, e altura AE de medida 3x/4.

Se o volume dessa pirâmide é igual a 54 cm³ , x é igual a

A

7 cm.

B

6 cm.

C

D

E

a678f8de-d8

IFF 2016 - Matemática - Pirâmides, Geometria Espacial

Os poliedros são figuras geométricas que apresentam todas as faces planas, como mostra a planificação a seguir. Montando a planificação, obtém-se uma pirâmide de base quadrangular.

Na figura, a área de sua base é igual à 12 cm² e as faces laterais da pirâmide são triângulos equiláteros, a área total da pirâmide é:

A

12(2+√3) cm² .

B

12(1+√3) cm² .

C

12(1+√2) cm² .

D

30 cm².

E

36 cm² .

09cf07dd-bb

UECE 2014 - Matemática - Pirâmides, Geometria Espacial

O número total de arestas de uma pirâmide que tem exatamente 17 faces, incluindo a base, é

A

34.

B

30.

C

26.

D

32.

864155b4-c6

UECE 2013 - Matemática - Pirâmides, Geometria Espacial

Sejam X, Y e Z três pontos fixos distintos e não colineares, e P um ponto do espaço, vértice de uma pirâmide cuja base é o triângulo XYZ e cuja medida do seu volume é 3 m3 . O conjunto de todos os pontos P que cumprem esta condição é formado por

A

duas retas paralelas.

B

um plano.

C

dois planos.

D

exatamente dois pontos.

850a1052-c6

UFSC 2010 - Matemática - Pirâmides, Geometria Espacial

Assinale a proposição CORRETA.

A altura da pirâmide cuja secção transversal paralela à base está a 4 cm dessa (base) e tem uma área igual a 1/4 da área da base é 8 cm.

C

Certo

E

Errado

9c49bbbc-c5

UEG 2018 - Matemática - Pirâmides, Áreas e Perímetros, Geometria Plana, Geometria Espacial

Na aula de matemática, a professora mostrou um sólido no formato de uma pirâmide hexagonal regular, cuja aresta da base media l = 4 cm e a área lateral da pirâmide era de 60 cm2 . Em seguida, solicitou aos alunos que calculassem o volume dessa pirâmide. O valor encontrado foi de

A

V = 8√39 cm3

B

V = 6√39 cm3

C

V = √39 cm3

D

V = 4√39 cm3

E

V = 3v39 / 4 cm3

bb070525-ba

UERJ 2017, UERJ 2017, UERJ 2017 - Matemática - Pirâmides, Prismas, Geometria Espacial

A imagem a seguir ilustra um prisma triangular regular. Sua aresta da base mede b e sua aresta lateral mede h.
Esse prisma é seccionado por um plano BCP, de modo que o volume da pirâmide ABCP seja exatamente 1/9 do volume total do prisma.

Logo, a medida de AP é igual a:

A

h/9

B

h/3

C

2h/3

D

5h/6

f07023c7-b9

UERJ 2016, UERJ 2016 - Matemática - Pirâmides, Geometria Espacial

Uma pirâmide com exatamente seis arestas congruentes é denominada tetraedro regular. Admita que a aresta do tetraedro regular ilustrado a seguir, de vértices ABCD, mede 6 cm e que o ponto médio da aresta BC é M.
O cosseno do ângulo equivale a:

A

1/2

B

1/3

C

2/3

D

2/5

de53e116-b9

UECE 2016 - Matemática - Pirâmides, Geometria Espacial

Se a soma dos ângulos de todas as faces de uma pirâmide (incluindo a base) é 3600 graus, então, a base da pirâmide é um polígono com

A

9 lados.

B

10 lados.

C

11 lados.

D

12 lados.

0783762a-b6

UECE 2009 - Matemática - Pirâmides, Geometria Espacial

O número de arestas de uma pirâmide que tem 12 faces é

A

14

B

16

C

18

D

22

affc90d0-b1

UDESC 2017 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Pirâmides, Geometria Espacial

Uma pirâmide regular de base hexagonal tem o vértice sobre uma semiesfera e a base inscrita na base desta semiesfera. Sabendo que a aresta lateral dessa pirâmide mede 10 cm, então o volume é igual a:

A

125√6 cm3

B

500√3 cm3

C

375√6 cm3

D

5√15/2 cm3

E

250√3 cm3

e3e0ec29-b0

UDESC 2017 - Matemática - Sistema de Unidade de Medidas, Aritmética e Problemas, Esfera, Pirâmides, Cone, Prismas, Geometria Espacial, Cilindro, Poliedros

Em 1958, como trote para os calouros da universidade de Harvard, nos Estados Unidos, um grupo de estudantes precisou medir o comprimento da ponte de Harvard (entre Boston e Cambridge, em Massachusetts), usando como padrão de medida um dos próprios estudantes, um rapaz chamado Oliver R. Smoot. Após horas de medição, com o estudante deitando-se no chão e levantando-se sucessivas vezes para as medidas, concluiu-se que a ponte tinha 364,4 smoots, +/- 1 orelha.

A brincadeira fez tanto sucesso e a medição tornou-se tão popular que, na década de 1980, a ponte foi reformada pela prefeitura, que encomendou blocos de concreto personalizados de 1 smoot de comprimento para a reforma, eternizando as marcações colocadas no solo, que hoje já constam até no sistema de conversão de medidas da ferramenta Google.

Ainda mais interessante é o fato de que, alguns anos após formado, Oliver Smoot tornou-se diretor da ANSI, o Instituto Nacional Americano de Padrões (“American National Standards Institute”) e depois presidente da ISO, a Organização Internacional para Padronização (“International Organization for Standardization”).

Sabendo que Oliver Smoot tinha 5 pés e 7 polegadas de altura na ocasião da medida, desprezando o erro de +/- 1 orelha, e assumindo 1 pé = 30,5 cm e 1 polegada = 2,5 cm, o comprimento da ponte é:

A

600 m

B

619,48 m

C

633,51 m

D

111,14 m

E

117,85 m

4b9c214f-0a

ENEM 2019 - Matemática - Pirâmides, Geometria Espacial, Poliedros

As luminárias para um laboratório de matemática serão fabricadas em forma de sólidos geométricos. Uma delas terá a forma de um tetraedro truncado. Esse sólido é gerado a partir de secções paralelas a cada uma das faces de um tetraedro regular. Para essa luminária, as secções serão feitas de maneira que, em cada corte, um terço das arestas seccionadas serão removidas. Uma dessas secções está indicada na figura.

Essa luminária terá por faces

A

4 hexágonos regulares e 4 triângulos equiláteros.

B

2 hexágonos regulares e 4 triângulos equiláteros.

C

4 quadriláteros e 4 triângulos isósceles.

D

3 quadriláteros e 4 triângulos isósceles.

E

3 hexágonos regulares e 4 triângulos equiláteros.

d1340675-ba

UFRGS 2019 - Matemática - Pirâmides, Geometria Espacial

Considere o paralelepípedo de vértices A, B, C, D, E, F, G, H e a pirâmide de vértices B, F, G, H, inscrita no paralelepípedo, representados na figura a seguir.

A razão entre o volume da pirâmide e o volume do paralelepípedo é

NESTA PROVA, SERÃO UTILIZADOS OS SEGUINTES SÍMBOLOS E CONCEITOS COM OS RESPECTIVOS SIGNIFICADOS:

N: Conjunto dos números naturais.

R: Conjunto dos números reais.

A

1/6 .

B

1/5 .

C

1/4 .

D

1/3 .

E

1/2 .

db7914f7-cb

UECE 2017 - Matemática - Pirâmides, Geometria Espacial

A medida da altura de uma pirâmide é 10 m e sua base é um triângulo retângulo isósceles cuja medida da hipotenusa é 6 m. Pode-se afirmar corretamente que a medida do volume dessa pirâmide, em m3, é igual a

A

60.

B

30.

C

15.

D

45.

d60ba3fd-bb

UERJ 2018 - Matemática - Pirâmides, Geometria Espacial

Observe na imagem uma pirâmide de base quadrada, seccionada por dois planos paralelos à base, um contendo o ponto A e o outro o ponto B. Esses planos dividem cada aresta lateral em três partes iguais.

Considere as seguintes medidas da pirâmide:

• altura = 9 cm;
• aresta da base = 6 cm;
• volume total = 108 cm3 .

O volume da região compreendida entre os planos paralelos, em cm3 , é:

A

26

B

24

C

28

D

30

dc929f4c-a6

UFU-MG 2017 - Matemática - Pirâmides, Geometria Espacial

Um designer de jogos virtuais está simulando alguns deslocamentos associados com uma pirâmide quadrangular regular, em que o lado do quadrado da base mede 40 cm.

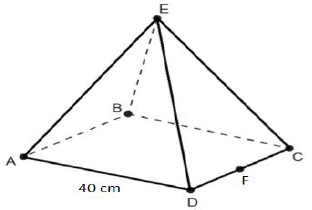
(Figura ilustrativa e sem escalas)

Ele simula a trajetória de um lagarto pelas faces da pirâmide. Inicialmente o lagarto desloca-se de A até E e, posteriormente, de E até F, em que F é o ponto médio de CD. Cada um desses dois trechos da trajetória ocorre em linha reta.

A projeção perpendicular dessa trajetória em ABCD, presente no plano da base da pirâmide, descreve uma curva R, a qual é a união de dois segmentos.

Nessas condições, o comprimento de R, em cm, é igual a

A

20 √2

B

40 √2

C

40 (1 + √2)

D

20 (1 + √2)

Questõessobre Pirâmides