Questõesde UEFS sobre Números Complexos
Considere a equação 2x2 − kx + k = 0, k ∈ R − {0}.
Escolhendo-se o coeficiente k aleatoriamente, dentre os elementos do conjunto
X = {−3, −1, 0, 1, 2, 4, 5, 7, 8}, a chance de a equação obtida ter raízes complexas é
Considerando-se os números complexos Z = cos 5π/3 +isen 5π/3 e W = cosπ/6 + isen π/6 , é correto afirmar
que o menor valor inteiro positivo de n que torna um número real positivo é
O conjunto X = {4m + 5n;m,n∈Z+} contém todos os números inteiros positivos
Sejam os números complexos z1 = sen 40º + i.cos 40º e z2 = cos 40º − i.sen 40º.
O argumento principal do número z1.z2 é igual a
Sejam os números complexos z1 = sen 40º + i.cos 40º e z2 = cos 40º − i.sen 40º.
O argumento principal do número z1.z2 é igual a
Considerando-se os números complexos  e
e  , é correto afirmar
que o menor valor inteiro positivo de n que torna
, é correto afirmar
que o menor valor inteiro positivo de n que torna  um número real positivo é
um número real positivo é
Considerando-se os números complexos  e
e  , é correto afirmar
que o menor valor inteiro positivo de n que torna
, é correto afirmar
que o menor valor inteiro positivo de n que torna  um número real positivo é
um número real positivo é
Sendo 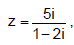 considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por
considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por
Sendo 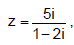 considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por
considere o número complexo w com módulo igual ao de z e argumento
principal medindo o dobro do argumento principal de z.
Nessas condições, w pode ser representado algebricamente por





Considerando-se os números complexos z = cos 5π/3 + isen 5π/3 e w = cos π/6 + isen π/6, é correto afirmar
que o menor valor inteiro positivo de n que torna  um número real positivo é
um número real positivo é
 um número real positivo é
um número real positivo éDiz-se que um número inteiro positivo x é um número perfeito, quando é a soma de todos
os seus divisores positivos, exceto ele próprio. Por exemplo, 28 é um número perfeito, pois
28 = 1 + 2 + 4 + 7 + 14. A última proposição do nono livro dos Elementos de Euclides prova
que se n é um inteiro positivo, tal que 2n
−1 é um número primo, então 2n–1(2n
−1) é um número
perfeito. Euler provou que todo número perfeito par tem essa forma, mas ainda não são
conhecidos números perfeitos ímpares.
O menor elemento do conjunto P = {n ∈ Z*+ / 2n−1(2n
−1) > 1128}, para o qual 2n–1(2n
−1) é um número
perfeito, é
O número complexo 1 + i é raiz do polinômio P(x) = x4 + 3x3
+ px2 − 2x + q, com p,q ∈R.
Então, a soma das raízes reais de P(x) é
O número complexo 1 + i é raiz do polinômio P(x) = x4 + 3x3 + px2 − 2x + q, com p,q ∈R.
Então, a soma das raízes reais de P(x) é
Considerem-se, no plano complexo representado na figura, os pontos P, Q e R pertencentes a uma circunferência de centro na origem.

Sendo P o afixo de z = 2 - 3/2i e QR, um arco medindo 5µ/12, pode-se afirmar que o ponto R é afixo do número complexo que pode ser representado, algebricamente, por
Considerem-se, no plano complexo representado na figura, os pontos P, Q e R pertencentes a uma circunferência de centro na origem.

Sendo P o afixo de z = 2 - 3/2i e QR, um arco medindo 5µ/12, pode-se afirmar que o ponto R é afixo do número complexo que pode ser representado, algebricamente, por