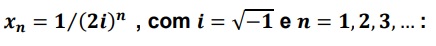Questõessobre Números Complexos

Os únicos números reais x que satisfazem a igualdade x = 1 + 1 / 1+ 1/1x são

Considerando que, no sistema de coordenadas cartesianas ortogonais xOy, cada ponto (x, y) do plano cartesiano seja identificado com um número complexo z = x + iy, em que (i)2 = -1, julgue o item. e faça o que se pede no item 122, que é do tipo C.

Assinale a opção que apresenta um dos valores de 3√i.

-i.

Considerando que, no sistema de coordenadas cartesianas ortogonais xOy, cada ponto (x, y) do plano cartesiano seja identificado com um número complexo z = x + iy, em que (i)2 = -1, julgue o item.

Se z1 = 1/2 [cos(15º) + i sen(15º)] e z2 = 3 [cos(45º) + i sen(45º)], então

Considerando que, no sistema de coordenadas cartesianas ortogonais xOy, cada ponto (x, y) do plano cartesiano seja identificado com um número complexo z = x + iy, em que (i)2 = -1, julgue o item.

Se o quadrado de vértices nos pontos tiver área igual a 36 unidades de área, então |z| = 2√3 unidades de comprimento.

Leia o texto a seguir.

Foi ali no meio da praça. [...] Zuzé Paraza, pintor reformado, tossiu sacudindo a magreza do seu todo corpo. Então, assim contam os que viram, ele vomitou um corvo vivo. O pássaro saiu inteiro das entranhas dele. [...] Estivera tanto tempo lá dentro que já sabia falar.

COUTO, Mia. O último aviso do corvo falador. In: Vozes anoitecidas. São Paulo: Companhia das Letras, 2015. p. 29.

Zuzé desafiou o corvo falador. De dentro de seu gabinete, Zuzé mostrou ao corvo a seguinte tabela.

Zuzé solicita ao corvo que pense em uma equação matemática que relacione, linha a linha, os números das colunas A, B e C da tabela. Prontamente o corvo falante responde: iA+B = iC, onde i é a unidade imaginária.

Com base na equação dita pelo corvo e sabendo que A, B e C são números naturais, considere as afirmativas a seguir.

I. Se A + B é múltiplo de 4 e C = 4, então A, B e C satisfazem a equação.

II. Se A = 26, B = 44 e C = 30, então A, B e C satisfazem a equação.

III. Se A = B = 1, então a única possibilidade para que A, B e C satisfaçam a equação é C = 6.

IV. Se A e B são números ímpares e C = 1, então A, B e C satisfazem a equação.

Assinale a alternativa correta.

Uma estratégia para obter efeito humorístico em quadrinhos é atribuir a objetos abstratos características e ações tipicamente humanas. A figura a seguir é um exemplo de aplicação desse recurso.

Supondo que cada número diga uma verdade matemática sobre si mesmo, relacione as frases (de I a IV) aos balões de diálogo (de A a D).

I. Meu cubo é irracional.

II. Sou racional.

III. Sou puramente imaginário.

IV. Meu inverso multiplicativo coincide com meu conjugado.

Assinale a alternativa que contém a associação correta.

Considere as seguintes afirmações sobre números complexos.

I) (2 + i) (2 - i) (1 + i) (1 - i) = 10 .

II)

III) Se o módulo do número complexo z é 5, então o módulo de 2z é 10.

Quais afirmações estão corretas?

Considere as seguintes afirmativas a respeito da sequência de números 

1. O quinto elemento dessa sequência pode ser escrito na forma 

2. xn é um número imaginário puro, qualquer que seja n = 1,2,3, ...

3. |xn|se aproxima de zero conforme n cresce.

Assinale a alternativa correta.

Analise as seguintes afirmações a respeito dos números complexos:

I. Um número complexo Z é um número que pode ser escrito da forma z = x + yi, com x e y reais e i = √-1 .

II. Todo número complexo é um número real.

III. Todo número real é um número complexo.

IV. Seja z = 6 + 8i, então |z| = 10.

Uma cancha de futsal está situada sobre um sistema de coordenadas do plano complexo (Argand Gauss), com unidades marcadas em metros e com centro sobre o ponto (0, 0), como na figura abaixo. Se a circunferência central possui uma área de 9 π m2 , a expressão que melhor representa esta circunferência central, em z∈ℂ, é