Para algum temos que e ∈ R - Q temos que i = 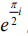 , onde é
a unidade imaginária. Então, é CORRETO afirmar que i i pertence a
, onde é
a unidade imaginária. Então, é CORRETO afirmar que i i pertence a
Para algum temos que e ∈ R - Q temos que i = 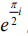 , onde é
a unidade imaginária. Então, é CORRETO afirmar que i i pertence a
, onde é
a unidade imaginária. Então, é CORRETO afirmar que i i pertence a

 é a unidade imaginária dos números complexos, tem-se que,
das afirmações a seguir,
é a unidade imaginária dos números complexos, tem-se que,
das afirmações a seguir, (conjugado de z), são tais
que os pontos de intersecção dos lugares geométricos que representam
as soluções das equações z .
(conjugado de z), são tais
que os pontos de intersecção dos lugares geométricos que representam
as soluções das equações z .