Dada a matriz A(x) = 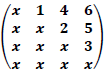 considere p(x) = detA(x) em que “det” denota o determinante.
Então o polinômio p(x) pode ser fatorado como
considere p(x) = detA(x) em que “det” denota o determinante.
Então o polinômio p(x) pode ser fatorado como
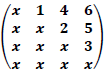 considere p(x) = detA(x) em que “det” denota o determinante.
Então o polinômio p(x) pode ser fatorado como
considere p(x) = detA(x) em que “det” denota o determinante.
Então o polinômio p(x) pode ser fatorado como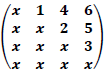 considere p(x) = detA(x) em que “det” denota o determinante.
Então o polinômio p(x) pode ser fatorado como
considere p(x) = detA(x) em que “det” denota o determinante.
Então o polinômio p(x) pode ser fatorado como à direita pela matriz
à direita pela matriz  e
transmite o resultado
e
transmite o resultado  na sequência x, y, v, w.
Por exemplo, a sequência 1, 8, 11, 3 é transmitida
como a sequência 10, 19, 25, 39. Então,
na sequência x, y, v, w.
Por exemplo, a sequência 1, 8, 11, 3 é transmitida
como a sequência 10, 19, 25, 39. Então,Em um torneio de vôlei, as equipes A, B, C e D obtiveram os resultados registrados na tabela a seguir.

Sabendo-se que cada resultado, pelo regulamento do torneio, tem a pontuação correspondente segundo a tabela a seguir, a matriz que corresponde à pontuação total no torneio de cada equipe é







A soma dos cofatores dos elementos da diagonal secundária da
matriz 
Três modelos de aparelhos de ar-condicionado, I, II e III, de diferentes potências, são produzidos por um determinado fabricante.
Uma consulta sobre intenção de troca de modelo foi realizada com 1000 usuários desses produtos. Observe a matriz A , na qual cada elemento aij representa o número daqueles que pretendem trocar do modelo i para o modelo j.

Escolhendo-se aleatoriamente um dos usuários consultados, a probabilidade de que ele não pretenda trocar seu modelo de ar-condicionado é igual a:
 for maior do que zero, então
for maior do que zero, então Considere as seguintes matrizes:  Assinale a alternativa correta:
Assinale a alternativa correta:
 , em que x e y
são números reais. Se det(M) representa o
determinante da matriz M, então, em um plano com o
sistema de coordenadas cartesiano usual, a equação
det(M) = – 4 expressa a equação de uma reta. A
distância dessa reta à origem do sistema de
coordenadas é igual a
, em que x e y
são números reais. Se det(M) representa o
determinante da matriz M, então, em um plano com o
sistema de coordenadas cartesiano usual, a equação
det(M) = – 4 expressa a equação de uma reta. A
distância dessa reta à origem do sistema de
coordenadas é igual aConsidere as matrizes A = 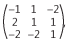 , B =
, B = 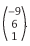 e C =
e C = 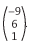 .
.
Sabendo-se que A . B = C, afirma-se:
Considere a seguinte matriz: A =
Sabendo que 0 ≤ x ≤ π/2 e cos (x) = 12/13, qual dos valores abaixo mais se aproxima do determinante da matriz?




 matrizes e f uma função dada por
f(x) = x2
– 2x + 3; então f(A) é:
matrizes e f uma função dada por
f(x) = x2
– 2x + 3; então f(A) é:




 e a função f : R → R definida por
f(x) = 1/3 det(A). Se f(3) = 3, o valor de k é:
e a função f : R → R definida por
f(x) = 1/3 det(A). Se f(3) = 3, o valor de k é: