Para qual valor de a a equação matricial
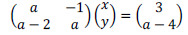
não admite solução?
Para qual valor de a a equação matricial
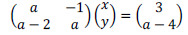
não admite solução?
Para qual valor de a a equação matricial
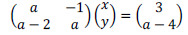
não admite solução?
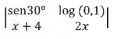 é nulo para o
seguinte valor de x:
é nulo para o
seguinte valor de x:Dadas as matrizes 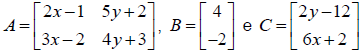 e sabendo que
A . B = C, então o valor de
x + y é igual a:
e sabendo que
A . B = C, então o valor de
x + y é igual a:
Podemos associar a cada elemento do grupo P(3) uma matriz que obedece às mesmas regras de multiplicação da tabela da questão 16. Considere que

As matrizes C, D e F são, respectivamente,
Do ponto de vista da Matemática, um Grupo é uma coleção de elementos (A, B, C, …) e uma regra de multiplicação que satisfazem as seguintes condições:
1. O produto de dois elementos quaisquer do Grupo resulta em um elemento do Grupo.
2. A multiplicação é associativa: (AB)C = A(BC).
3. Existe o elemento Identidade E de tal forma que AE = EA = A é válido para todos os elementos do Grupo.
4. Para todo elemento A, existe um elemento inverso A-1 de tal forma que AA-1 = A-1A = E.
Considere o Grupo P(3) formado pelas permutações de três números distintos.
Há 3! = 6 permutações diferentes possíveis de serem realizadas com três números distintos. Cada permutação é um elemento de P(3). Tais permutações estão indicadas abaixo. A linha superior indica o arranjo inicial e a linha de baixo indica o arranjo final para cada uma das 6 permutações.

Como podemos perceber, AB = D. Ou seja, ao realizar a
permutação A após a permutação B, teremos como
resultado a permutação D. Relações desse tipo definem
uma tabela de multiplicação para os 6 elementos do grupo
P (3).












Considere que a matriz diagonal  representa uma transformação linear (de R3 para R3) na
base {(-1,-1,2),(0,0,1),(-1,0,2)}. A matriz A’, que representa
a mesma transformação linear na base canônica, tem
como determinante e traço, respectivamente,
representa uma transformação linear (de R3 para R3) na
base {(-1,-1,2),(0,0,1),(-1,0,2)}. A matriz A’, que representa
a mesma transformação linear na base canônica, tem
como determinante e traço, respectivamente,
Considere a matriz quadrada de ordem 2,  cujos termos são definidos por aij = i − j − 2. Uma reta que passa pelo
ponto P = (a11, a22), e que tenha coeficiente
angular igual ao determinante de A, pode ser
representada graficamente por
cujos termos são definidos por aij = i − j − 2. Uma reta que passa pelo
ponto P = (a11, a22), e que tenha coeficiente
angular igual ao determinante de A, pode ser
representada graficamente por







 é a matriz inversa
de B e C =
é a matriz inversa
de B e C =  , o determinante de A é
, o determinante de A é como
sendo o número de combinações de n elementos
tomados p a p, qual o valor de x que satisfaz a
equação abaixo
como
sendo o número de combinações de n elementos
tomados p a p, qual o valor de x que satisfaz a
equação abaixo

 , o valor real de a para que o determinante da
matriz A2 + 2A seja igual a zero é:
, o valor real de a para que o determinante da
matriz A2 + 2A seja igual a zero é:


Sejam d(x) e D(x) respectivamente os
determinantes das matrizes m =

 onde y = senx, com x pertencendo
ao intervalo fechado [0,2 π]. Se n é o número de
valores de x tais que d(x) + D(x) = 0, então, é
correto afirmar que n é igual a
onde y = senx, com x pertencendo
ao intervalo fechado [0,2 π]. Se n é o número de
valores de x tais que d(x) + D(x) = 0, então, é
correto afirmar que n é igual a
Considerando-se a matriz M =  e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a
e sua transposta Mt, pode-se afirmar que a matriz soma (M + Mt) é igual a






 os números reais x1, x2 ,x3 e x4 formam, nessa ordem, uma progressão
geométrica crescente cujo primeiro termo é maior
do que zero. Se q é a razão dessa progressão, é
correto afirmar que o determinante da matriz M
(detM) satisfaz a dupla desigualdade
os números reais x1, x2 ,x3 e x4 formam, nessa ordem, uma progressão
geométrica crescente cujo primeiro termo é maior
do que zero. Se q é a razão dessa progressão, é
correto afirmar que o determinante da matriz M
(detM) satisfaz a dupla desigualdadeConsiderando-se as matrizes L = M =
M = e N =
e N =  após análise das proposições a seguir, assinale V para as verdadeiras e F, para as falsas.
após análise das proposições a seguir, assinale V para as verdadeiras e F, para as falsas.
( ) L−1
= 1/4 
( ) 3M + Nt
= 
( ) O determinante de L é 6.
( ) O sistema S = M tem infinitas soluções.
tem infinitas soluções.
A alternativa que indica a sequência correta, de cima para baixo, é a
Se a matriz 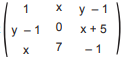 é simétrica, então o valor de xy é
é simétrica, então o valor de xy é