O valor de
x . y com x,y 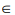 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
O valor de
x . y com x,y 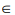 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:


O valor de
x . y com x,y 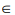 Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:
Z, sabendo que log2 (x) + log4 (y) = 2 e 2x+y = 32, é igual a:


Na escala Richter, as indicações R1 e R2 de dois terremotos estão relacionadas pela fórmula R1 - R2 = log10 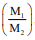 , em que M1 e M2 medem a energia liberada pelos terremotos sob a forma de ondas que
se propagam pela crosta terrestre. Houve dois terremotos: um correspondente a R1 = 8 e outro correspondente a
R2 = 6 . Nessas condições, a razão M1/M2 é igual a:
, em que M1 e M2 medem a energia liberada pelos terremotos sob a forma de ondas que
se propagam pela crosta terrestre. Houve dois terremotos: um correspondente a R1 = 8 e outro correspondente a
R2 = 6 . Nessas condições, a razão M1/M2 é igual a:
Existem alguns esportes em que a sensação de liberdade e perigo convivem lado a lado. Este é o caso do esqui na neve. Suponha que um esquiador, ao descer uma montanha, seja surpreendido por uma avalanche que o soterra totalmente. A partir do instante em que ocorreu o soterramento, a temperatura de seu corpo decresce ao longo do tempo t (em horas), segundo a função T(t) dada por
T(t) = ( T em graus Celsius), com t 0.
Quando a equipe de salvamento o encontra, já sem vida, a temperatura de seu corpo é de 12 graus Celsius. De acordo com as condições dadas, pode-se afirmar que ele ficou soterrado por, aproximadamente,
(Utilize a aproximação log3 2 0, = 6 )
A acidez de uma solução líquida é medida pela concentração de íons de hidrogênio H+ na solução. A medida de acidez usada é o pH, definido por
pH = - log10 [H+],
onde [H+] é a concentração de íons de hidrogênio. Se uma cerveja apresentou um pH de 4,0 e um suco de laranja, um pH de 3,0 , então, relativamente a essas soluções, é correto afirmar que a razão, (concentração de íons de hidrogênio na cerveja), quociente (concentração de íons de hidrogênio no suco), é igual a:
Com base nessas informações, julgue o próximo item.
Considerando-se que 0,7 é o valor aproximado para ln2, que
A = 10 bilhões e que P(2022) = 8 bilhões, então r > 0,05.
Estimar a quantidade de indivíduos da população mundial
futura é um desafio complexo. O modelo logístico baseia-se na
hipótese de que, com o passar dos anos, a população mundial deve
estabilizar-se em certo valor A ≠ 0, denominado população limite.
Segundo esse modelo, a população, P(t), de seres humanos no
planeta, em bilhões de habitantes, a partir de 1987, obedece
à equação  em que t é a quantidade de
anos a partir de 1987, que é o instante inicial e corresponde a t = 0;
5 bilhões é a população no ano de 1987; A é a população limite; e
r é uma constante positiva.
em que t é a quantidade de
anos a partir de 1987, que é o instante inicial e corresponde a t = 0;
5 bilhões é a população no ano de 1987; A é a população limite; e
r é uma constante positiva.
Com relação aos logaritmos, julgue o item abaixo.
Se a medida do lado de um quadrado for log3 x unidades de
comprimento e se a diferença entre o valor da área e o valor do
perímetro desse quadrado for igual a 5, então x > 240.
A Escala Richter é utilizada para medir a magnitude dos terremotos, permitindo-nos ter uma noção exata sobre o potencial dos abalos sísmicos que ocorrem na litosfera.
A Escala Richter é um sistema de medição elaborado por Charles Richter e Beno Gutenberg utilizado para quantificar a intensidade dos terremotos conforme a sua manifestação na superfície terrestre. Seu limite, teoricamente, não existe, mas é comum a convenção de que não haja terremotos que ultrapassem o grau 10.
De modo geral, podemos considerar que os abalos sísmicos acima de 6 podem ser considerados graves. Confira a seguir uma relação comparativa entre a intensidade dos terremotos e os seus efeitos:
A) Magnitude menor que 2: tremores captados apenas por sismógrafos.
B) Magnitude entre 2 e 4: impacto semelhante à passagem de um veículo grande e pesado.
C) Magnitude entre 4 e 6: quebra vidros, provoca rachaduras nas paredes e desloca móveis.
D) Magnitude entre 6 e 7: danos em edifícios e destruição de construções frágeis.
E) Magnitude entre 7 e 8: danos graves em edifícios e grandes rachaduras no solo.
F) Magnitude entre 8 e 9: destruição de pontes, viadutos e quase todas as construções.
G) Magnitude maior que 9: destruição total com ondulações visíveis.
A magnitude pode ser calculada pela seguinte equação:
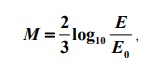
em que E0 é constante e vale 7.10-3 kWh, e E é a energia liberada no terremoto em kWh.
Se um terremoto teve E = 1 000 kWh, de energia liberada, a magnitude do terremoto está no
intervalo de:
Em março de 2011, um terremoto de 9,0 graus de
magnitude na escala Richter atingiu o Japão matando
milhares de pessoas e causando grande destruição.
Em janeiro daquele ano, um terremoto de 7,0 graus na
escala Richter atingiu a cidade de Santiago Del Estero,
na Argentina. A magnitude de um terremoto, medida
A
pela escala Richter, é  , em que A é a
amplitude do movimento vertical do solo, informado em
um sismógrafo, A0 é uma amplitude de referência e log
representa o logaritmo na base 10.
, em que A é a
amplitude do movimento vertical do solo, informado em
um sismógrafo, A0 é uma amplitude de referência e log
representa o logaritmo na base 10.
Disponível em: http://earthquake.usgs.gov. Acesso em: 28 fev. 2012 (adaptado).
A razão entre as amplitudes dos movimentos verticais dos terremotos do Japão e da Argentina é
A água comercializada em garrafões pode ser classificada como muito ácida, ácida, neutra, alcalina ou muito alcalina, dependendo de seu pH, dado pela expressão

em que H é a concentração de íons de hidrogênio, em mol por decímetro cúbico. A classificação da água de acordo com seu pH é mostrada no quadro.

Para o cálculo da concentração H, uma distribuidora mede dois parâmetros A e B, em cada fonte, e adota H como sendo o quociente de A por B. Em análise realizada em uma fonte, obteve A = 10-7 e a água dessa fonte foi classificada como neutra.
O parâmetro B, então, encontrava-se no intervalo
 10-6/7, 10-1
10-6/7, 10-1 
 10-1, 101/2
10-1, 101/2 
[1013, 10145)


Com o avanço em ciência da computação, estamos próximos do momento em que o número de transistores no processador de um computador pessoal será da mesma ordem de grandeza que o número de neurônios em um cérebro humano, que é da ordem de 100 bilhões.
Uma das grandezas determinantes para o desempenho de um processador é a densidade de transistores, que é o número de transistores por centímetro quadrado. Em 1986, uma empresa fabricava um processador contendo 100 000 transistores distribuídos em 0,25 cm2 de área. Desde então, o número de transistores por centímetro quadrado que se pode colocar em um processador dobra a cada dois anos (Lei de Moore).
Disponível em: www.pocket-lint.com. Acesso em: 1 dez. 2017 (adaptado).
Considere 0,30 como aproximação para log102.
Em que ano a empresa atingiu ou atingirá a densidade de 100 bilhões de transistores?
Um contrato de empréstimo prevê que quando uma parcela é paga de forma antecipada, conceder-se-á uma redução de juros de acordo com o período de antecipação. Nesse caso, paga-se o valor presente, que é o valor, naquele momento, de uma quantia que deveria ser paga em uma data futura. Um valor presente P submetido a juros compostos com taxa i, por um período de tempo n, produz um valor futuro V determinado pela fórmula
V = P ˑ (1 + i)n
Em um contrato de empréstimo com sessenta parcelas fixas mensais, de R$ 820,00, a uma taxa de juros de 1,32% ao mês, junto com a trigésima parcela será paga antecipadamente uma outra parcela, desde que o desconto seja superior a 25% do valor da parcela.
Utilize 0,2877 como aproximação para  e
0,0131 como aproximação para In (1,0132).
e
0,0131 como aproximação para In (1,0132).
A primeira das parcelas que poderá ser antecipada junto
com a 30ª é a
Leia o texto abaixo, sobre terremotos.
Magnitude é uma medida quantitativa do tamanho do terremoto. Ela está relacionada com a energia sísmica liberada no foco e também com a amplitude das ondas registradas pelos sismógrafos. Para cobrir todos os tamanhos de terremotos, desde os microtremores de magnitudes negativas até os grandes terremotos com magnitudes superiores a 8.0, foi idealizada uma escala logarítmica, sem limites. No entanto, a própria natureza impõe um limite superior a esta escala, já que ela está condicionada ao próprio limite de resistência das rochas da crosta terrestre. Magnitude e energia podem ser relacionadas pela fórmula descrita por Gutenberg e Richter em 1935: log(E) = 11,8 + 1,5 M onde: E = energia liberada em Erg ; M = magnitude do terremoto.
Disponível em:<http://www.iag.usp.br/siae98/terremoto/terremotos.htm >