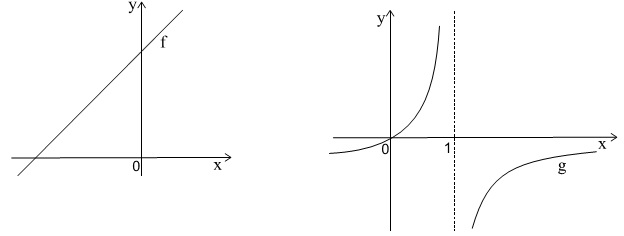Qual alternativa expressa o resultado do limite:

Qual alternativa expressa o resultado do limite:

Qual alternativa expressa o resultado do limite:

Leia o texto a seguir.
Luzia é de inestimável valor científico por se tratar do mais antigo fóssil humano paleoamericano já encontrado no Brasil. O crânio e ossos da coxa e do quadril de Luzia foram achados em 1975, em uma gruta da região de Lagoa Santa, em Minas Gerais. Seu esqueleto foi datado de 11,5 mil anos e ela deve ter morrido aos 25 anos. Neste século, seu rosto foi reconstituído na Inglaterra.
Adaptado de: www.museunacional.ufrj.br
Um dos processos de datação arqueológica ocorre calculando o porcentual r da quantidade de carbono 14 presente no fóssil em relação à quantidade desse mesmo elemento encontrada em um ser vivo de características semelhantes. Suponha que para fósseis humanos paleoamericanos a figura a seguir exiba o gráfico da função f : R∗ + → R+ que associa, a cada r, a quantidade t = f(r) de anos que se passaram desde a morte do ser humano em questão.

Com base no texto e no gráfico, assinale a alternativa
correta.



A classificação do som como forte ou fraco está relacionada ao nível de intensidade sonora, medida em watt/m². A menor intensidade sonora audível ou limiar de audibilidade possui intensidade I0=10–12W/m². A relação entre as intensidades sonoras permite calcular o nível sonoro do ambiente que é dado em decibéis. Em virtude dos valores das intensidades serem muito pequenos ou muito grandes, utiliza-se as noções de logaritmos na seguinte fórmula capaz de calcular níveis sonoros:

onde:
NS = Nível sonoro
I = Intensidade de som considerada
I0 = Limiar de audibilidade
Disponível em:<http://mundoeducacao.bol.uol.com.br/matematica/medindo-intensidade-dos-sons>





 é
representado por:
é
representado por:




Suponhamos que durante o mês de fevereiro de 2016 o crescimento exponencial seja dado pela fórmula P(t) = P(0) er.t , onde P(t) é a população infectada após t semanas e P(0) representa a quantidade de pessoas inicialmente infectadas.
Se após as duas primeiras semanas de fevereiro a quantidade de pessoas infectadas dobrou e usando ln(2) = 0,7 pode-se afirmar que o valor da constante r é
Uma pesquisa feita em São Paulo acerca do avanço da dengue pela Secretaria Municipal de Saúde (SMS), constatou que de 01/01/2016 até o dia 12/03/2016 o número de pessoas infectadas supera em 92% o total registrado no mesmo período do ano passado. O monitoramento semanal feito pela SMS mostra um crescimento exponencial do problema.
http://vejasp.abril.com.br/materia/dengue-rotina-paulistanos
 f(x) = 0, então
f(x) = 0, então  (sen f(x))n+1/ (f(x))n = 0.
(sen f(x))n+1/ (f(x))n = 0.