Quatro tanques cilíndricos são vistos de cima (em planta
baixa) conforme a figura. Todos têm 10 m de raio e seus
centros se posicionam em vértices dos dois quadrados
tracejados adjacentes, ambos com 30 m de lado. Uma fita de
isolamento, esticada e paralela ao solo, envolve os 4 tanques,
dando uma volta completa (linha em laranja na figura).

O comprimento da fita, em metros, é:
Quatro tanques cilíndricos são vistos de cima (em planta baixa) conforme a figura. Todos têm 10 m de raio e seus centros se posicionam em vértices dos dois quadrados tracejados adjacentes, ambos com 30 m de lado. Uma fita de isolamento, esticada e paralela ao solo, envolve os 4 tanques, dando uma volta completa (linha em laranja na figura).

O comprimento da fita, em metros, é:

















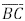 e
e 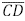 . Os segmentos
. Os segmentos 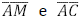 interceptam o segmento
interceptam o segmento 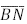 nos pontos
nos pontos 