Questõesde UNESP sobre Geometria Plana

InícioTodas as questões
1
1
1
Foram encontradas 24 questões
fff5d902-6a
UNESP 2021 - Matemática - Áreas e Perímetros, Geometria Plana

Durante o surto de covid-19, diversas reportagens procuraram explicar o ritmo de infecções causadas pelo coronavírus nos estados brasileiros. Uma delas mostrou que, nos primeiros 30 dias da pandemia, nos estados que apresentaram maior rapidez de contaminação, o contágio ficou caracterizado por duplicar o número de infectados em um período de tempo variando de 3 a 5 dias. A partir dessa informação, o ilustrador de um jornal sugeriu o esquema seguinte para mostrar a diferença entre os ritmos de contágio.



Dado que a área dos círculos representa o número de infectados e que o círculo inicial possui raio unitário, quais devem ser os valores de r e de R para que a imagem represente corretamente o crescimento indicado nas setas?

A
r = 8 e R = 16.
B
r = 6 e R = 10.
C
r = 8 e R = 32.
D
r = 6 e R = 12.
E
r = 64 e R = 1024.
ffe5d916-6a
UNESP 2021 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales

Na aviação, o perímetro da região que define a fase final da manobra de aproximação para um helicóptero pairar ou pousar pode ser definido por meio de sinalizadores uniformemente espaçados. As características dimensionais desses sinalizadores de perímetro estão indicadas na figura a seguir.



Uma empresa contratada para produzir esse sinalizador está definindo os parâmetros para a produção em escala do artefato. Para tanto, é necessário conhecer o valor do ângulo b de abertura do sinalizador, indicado na figura, respeitadas as medidas nela apresentadas.

Considere a tabela trigonométrica a seguir.



De acordo com a tabela, o ângulo b necessário para a produção do sinalizador é igual a:

A
126,8º
B
120,0º
C
116,5º
D
150,0º
E
107,1º
1bd254a9-b9
UNESP 2019 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales

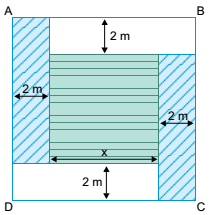
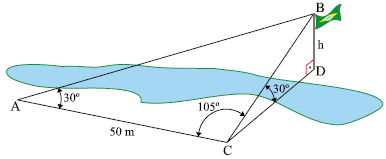
Uma das finalidades da Ciência Forense é auxiliar nas investigações relativas à justiça civil ou criminal. Observe uma ideia que pode ser empregada na análise de uma cena de crime.


Uma gota de sangue que cai perfeitamente na vertical, formando um ângulo de 90º com a horizontal, deixa uma mancha redonda. À medida que o ângulo de impacto com a horizontal diminui, a mancha fica cada vez mais longa.


As ilustrações mostram o alongamento da gota de sangue e a relação trigonométrica envolvendo o ângulo de impacto e suas dimensões.



Alongamento da gota de sangue



Relação trigonométrica


(Ana Paula Sebastiany et al. “A utilização da Ciência Forense e da

Investigação Criminal como estratégia didática na compreensão de

conceitos científicos”. Didáctica de la Química, 2013. Adaptado.)



Considere a coleta de uma amostra de gota de sangue e a tabela trigonométrica apresentadas a seguir.





De acordo com as informações, o ângulo de impacto da gota de sangue coletada na amostra foi de

A
37º
B
74º
C
59º
D
53º
E
31º
92f0c845-af
UNESP 2013 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales

A caçamba de um caminhão basculante tem 3 m de comprimento das direções de seu ponto mais frontal P até a de seu eixo de rotação e 1 m de altura entre os pontos P e Q. Quando na posição horizontal, isto é, quando os segmentos de retas r e s se coincidirem, a base do fundo da caçamba distará 1,2 m do solo. Ela pode girar, no máximo, α graus em torno de seu eixo de rotação, localizado em sua parte traseira inferior, conforme indicado na figura.

(www.autobrutus.com. Adaptado.)

Dado cos α = 0,8, a altura, em metros, atingida pelo ponto P, em relação ao solo, quando o ângulo de giro α for máximo, é

A
4,8.
B
5,0.
C
3,8.
D
4,4.
E
4,0.
92d4aa1a-af
UNESP 2013 - Matemática - Pontos e Retas, Circunferências e Círculos, Geometria Analítica, Geometria Plana

Uma partícula em movimento descreve sua trajetória sobre semicircunferências traçadas a partir de um ponto P0 , localizado em uma reta horizontal r, com deslocamento sempre no sentido horário. A figura mostra a trajetória da partícula, até o ponto P3 , em r. Na figura, O, O1 e O2 são os centros das três primeiras semicircunferências traçadas e R, R/2 e R/4 seus respectivos raios.



A trajetória resultante do movimento da partícula será obtida repetindo-se esse comportamento indefinidamente, sendo o centro e o raio da n-ésima semicircunferência dados por On e Rn = R/2n , respectivamente, até o ponto Pn , também em r. Nessas condições, o comprimento da trajetória descrita pela partícula, em função do raio R, quando n tender ao infinito, será igual a 

A
2² · π · R.
B
2³ · π · R.
C
2n · π · R.
D
(7/4) . π · R.
E
2 · π · R.
0024946a-0a
UNESP 2018 - Matemática - Geometria Plana, Triângulos

Uma criança está sentada no topo de um escorregador cuja estrutura tem a forma de um triângulo ABC, que pode ser perfeitamente inscrito em um semicírculo de diâmetro AC = 4 m. O comprimento da escada do escorregador é AB = 2 m.


Considerando que a energia potencial gravitacional da criança no ponto B, em relação ao solo horizontal que está em , é igual a 342 joules, e adotando , a massa da criança é igual a

A
30 kg.
B
25 kg.
C
20 kg.
D
24 kg.
E
18 kg.
332bac6d-58
UNESP 2018 - Matemática - Quadriláteros, Funções, Geometria Plana, Polinômios, Função de 2º Grau

Sendo x um número real maior que 2/3 , a área de um retângulo é dada pelo polinômio 3x2 + 19x –14. Se a base desse retângulo é dada pelo polinômio x + 7, o quadrado da diagonal do retângulo é expresso pelo polinômio

A
10x2 + 26x + 29.
B
10x2 + 53.
C
10x2 + 65.
D
4x2 + 2x + 53.
E
10x2 + 2x + 53.
33331c05-58
UNESP 2018 - Matemática - Áreas e Perímetros, Progressão Aritmética - PA, Quadriláteros, Geometria Plana, Progressões

A figura mostra cinco retângulos justapostos de uma sequência. Todos os retângulos possuem mesma altura, igual a 1 cm.



Sabendo que 1 m2 equivale a 10000 cm2 e que a sequência é constituída por 100 retângulos, a figura formada tem área igual a

A
2,5 m2 .
B
4 m2 .
C
5 m2 .
D
2 m2 .
E
4,5 m2 .
341f4c27-1b
UNESP 2017 - Matemática - Aritmética e Problemas, Áreas e Perímetros, Porcentagem, Quadriláteros, Geometria Plana

Os estudantes 1, 2 e 3 concorreram a um mesmo cargo da diretoria do grêmio de uma faculdade da UNESP, sendo que 1 obteve 6,25% do total de votos que os três receberam para esse cargo. Na figura, a área de cada um dos três retângulos representa a porcentagem de votos obtidos pelo candidato correspondente. Juntos, os retângulos compõem um quadrado, cuja área representa o total dos votos recebidos pelos três candidatos.



Do total de votos recebidos pelos três candidatos, o candidato 2 obteve

A
61,75%.
B
62,75%.
C
62,50%.
D
62,00%.
E
62,25%.
45aa8b4e-3c
UNESP 2015 - Matemática - Polígonos, Geometria Plana

Os polígonos ABC e DEFG estão desenhados em uma malha formada por quadrados. Suas áreas são iguais a S1 e S2, respectivamente, conforme indica a figura.
Sabendo que os vértices dos dois polígonos estão exatamente sobre pontos de cruzamento das linhas da malha, é correto afirmar que S2/S1 é igual a

A
5,25.
B
4,75.
C
5,00.
D
5,50.
E
5,75.
c6b7d14a-3b
UNESP 2017 - Matemática - Polígonos, Geometria Plana

Os polígonos SOL e LUA são triângulos retângulos isósceles congruentes. Os triângulos retângulos brancos no interior de SOL são congruentes, assim como também são congruentes os triângulos retângulos brancos no interior de LUA.


A área da superfície em amarelo e a área da superfície em azul estão na mesma unidade de medida. Se x é o número que multiplicado pela medida da área da superfície em amarelo resulta a medida da área da superfície em azul, então x é igual a

A
16/15
B
15/16
C
9/10
D
24/25
E
25/24
1b4e0489-30
UNESP 2016 - Matemática - Polígonos, Geometria Plana

O hexágono marcado na malha quadriculada sobre a fotografia representa o contorno do câmpus da Unesp de Rio Claro, que é aproximadamente plano.
A área aproximada desse câmpus, em km2 , é um número pertencente ao intervalo

A
[0,8 ; 1,3[
B
[1,8 ; 2,3[
C
[2,3 ; 2,8[
D
[1,3 ; 1,8[
E
[0,3 ; 0,8[
cfa765c7-29
UNESP 2016 - Matemática - Áreas e Perímetros, Geometria Plana, Geometria Espacial, Poliedros

Um cubo com aresta de medida igual a x centímetros foi seccionado, dando origem ao prisma indicado na figura 1. A figura 2 indica a vista superior desse prisma, sendo que AEB é um triângulo equilátero.

 

              


Sabendo-se que o volume do prisma da figura 1 é igual a 2(4 - √3)cm3 , x é igual a

A
2
B
7/2
C
3
D
5/2
E
3/2
cf9e6f40-29
UNESP 2016 - Matemática - Geometria Plana, Ângulos - Lei Angular de Thales

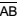Uma mesa de passar roupa possui pernas articuladas  e 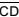, conforme indica a figura. Sabe-se que AB = CD = 1 m, e que M é ponto médio dos segmentos coplanares 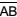e 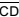. Quando a mesa está armada, o tampo fica paralelo ao plano do chão e a medida do ângulo 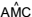é 60º.

                       


Considerando-se desprezíveis as medidas dos pés e da espessura do tampo e adotando √3 = 1,7, a altura do tampo dessa mesa armada em relação ao plano do chão, em centímetros, está entre

A
96 e 99.
B
84 e 87.
C
80 e 83.
D
92 e 95.
E
88 e 91.
cf9a5741-29
UNESP 2016 - Matemática - Áreas e Perímetros, Geometria Plana

Em um terreno retangular ABCD, de 20 m2 , serão construídos um deque e um lago, ambos de superfícies retangulares de mesma largura, com as medidas indicadas na figura. O projeto de construção ainda prevê o plantio de grama na área restante, que corresponde a 48% do terreno.

No projeto descrito, a área da superfície do lago, em m2 , será igual a

A
4,1.
B
4,2.
C
3,9.
D
4,0.
E
3,8.
4a5dcaa6-a4
UNESP 2015 - Matemática - Áreas e Perímetros, Quadriláteros, Geometria Plana

Renata pretende decorar parte de uma parede quadrada ABCD com dois tipos de papel de parede, um com linhas diagonais e outro com riscos horizontais. O projeto prevê que a parede seja dividida em um quadrado central, de lado x, e quatro retângulos laterais, conforme mostra a figura.

                                       

Se o total da área decorada com cada um dos dois tipos de papel é a mesma, então x, em metros, é igual a


A
1 + 2√3
B
2 + 2√3
C
2 + √3
D
1 + √3
E
4 + √3
06251d2b-8d
UNESP 2010 - Matemática - Geometria Plana, Triângulos

ma pessoa se encontra no ponto A de uma planície, às margens de um rio e vê, do outro lado do rio, o topo do mastro de uma bandeira, ponto B. Com o objetivo de determinar a altura h do mastro, ela anda, em linha reta, 50 m para a direita do ponto em que se encontrava e marca o ponto C. Sendo D o pé do mastro, avalia que os ângulos BÂC e BĈD valem 30º, e o ângulo AĈB vale 105º, como mostra a figura.

  

A altura h do mastro da bandeira, em metros, é:

A
12,5.
B
12,5 √2.
C
25,0.
D
25,0 √2 .
E
35,0.
f130e431-36
UNESP 2012 - Matemática - Circunferências e Círculos, Geometria Plana

No vazamento de petróleo da empresa americana Chevron do último dia 7 de novembro, na bacia de Campos/RJ, a mancha de óleo na superfície do mar assumiu grandes dimensões e teve seu pico de área entre os dias 12 e 14 daquele mês. O vazamento levou dias para ser contido, pois o petróleo continuava a escapar por fissuras, como mostrado na foto.

Dados 1 dm3 = 1 L e π ≈ 3 e sabendo que a altura média da lâmina de óleo sobre as águas era de 0,003 mm e que 1 barril de petróleo cru contém 160 litros de óleo, o número aproximado de barris que vazaram no incidente foi

A
2360.
B
2860
C
2960.
D
3320.
E
5250.
115f0edb-36
UNESP 2010 - Matemática - Pontos e Retas, Relações Métricas no Triângulo Retângulo, Geometria Analítica, Geometria Plana, Ângulos - Lei Angular de Thales

Em um experimento sobre orientação e navegação de pombos,considerou-se o pombal como a origem O de um sistema de coordenadas cartesianas e os eixos orientados Sul-Norte (SN) e Oeste-Leste (WL). Algumas aves foram liberadas num ponto P que fica 52 km ao leste do eixo SN e a 30 km ao sul do eixo WL. O ângulo azimutal de P é o ângulo, em graus, medido no sentido horário a partir da semirreta ON até a semirreta OP. No experimento descrito, a distância do pombal até o ponto de liberação das aves, em km, e o ângulo azimutal, em graus, desse ponto são,respectivamente:

Dado: √3604 ≈ 60.



A
42,5 e 30.
B
42,5 e 120.
C
60 e 30.
D
60 e 120.
E
60 e 150.
113ba182-36
UNESP 2010 - Matemática - Circunferências e Círculos, Geometria Plana

Uma aeronave faz sua aproximação final do destino, quando seu comandante é informado pelo controlador de voo que, devido ao intenso tráfego aéreo, haverá um tempo de espera de 15 minutos para que o pouso seja autorizado e que ele deve permanecer em rota circular, em torno da torre de controle do aeroporto, a 1500 metros de altitude, até que a autorização para o pouso seja dada. O comandante, cônscio do tempo de espera a ser despendido e de que, nessas condições, a aeronave que pilota voa a uma velocidade constante de Vc (km/h), decide realizar uma única volta em torno da torre de controle durante o tempo de espera para aterrissar.

Sabendo que o aeroporto encontra-se numa planície e tomando sua torre de controle como sendo o ponto de origem de um sistema de coordenadas cartesianas, determine a equação da projeção ortogonal, sobre o solo, da circunferência que a aeronave descreverá na altitude especificada.



A


B


C


D


E