8dabac36-dc
UFRN 2011, UFRN 2011, UFRN 2011 - Matemática - Quadriláteros, Geometria Plana
Em um experimento, uma aranha é colocada dentro de uma caixa, sem tampa, em um ponto A e
estimulada a caminhar até o ponto B, onde se encontra um alimento. O seu trajeto , sempre em
linha reta, é feito pelas paredes e pelo piso da caixa, passando pelos pontos P e Q, conforme
ilustra a Figura 1. A Figura 2 mostra a mesma caixa recortada e colada sobre uma mesa.

De acordo com a Figura 2, onde AB é um segmento de reta, pode-se afirmar que a trajetória
Em um experimento, uma aranha é colocada dentro de uma caixa, sem tampa, em um ponto A e
estimulada a caminhar até o ponto B, onde se encontra um alimento. O seu trajeto , sempre em
linha reta, é feito pelas paredes e pelo piso da caixa, passando pelos pontos P e Q, conforme
ilustra a Figura 1. A Figura 2 mostra a mesma caixa recortada e colada sobre uma mesa.

De acordo com a Figura 2, onde AB é um segmento de reta, pode-se afirmar que a trajetória
A
utilizada pela aranha é a menor possível.
B
correspondente ao segmento AB é a menor possível.
C
utilizada pela aranha é a maior possível.
D
correspondente ao segmento AB é maior que a utilizada pela aranha.
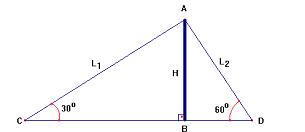
 , fixados nos pontos C e D, respectivamente.
, fixados nos pontos C e D, respectivamente. 
 que usou para fixar a torre.
que usou para fixar a torre.  e
e  é
é 
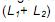 que usou para fixar a torre.
que usou para fixar a torre.